DSO的前端跟踪

DSO中的前端跟踪过程相对简单，其主要涵盖跟踪前处理、跟踪过程和跟踪后处理三部分内容。下面我会对这三部分进行拆解并对其中的细节进行介绍。

1. 参考帧确定和跟踪参考点构建（跟踪前处理）

当DSO系统的初始化完成后，目前整个系统中会有两个关键帧和若干激活地图点，当然激活地图点的host帧为初始化参考帧。和初始化过程类似，由于新来的一帧frame的位姿不明确，需要一个相对鲁邦的位姿估计方法，和初始化过程一样，DSO的前端跟踪部分采用的也是基于金字塔由粗至精的跟踪方法，因此需要确定一个跟踪参考帧和若干跟踪地图点。

在介绍参考点构建之前，我先明确一个问题，就是DSO系统会维护一个关键帧队列，即DSO中的关键帧滑动窗口，至于这个滑窗的维护策略，我会在后续文章中进行介绍。

1.1 金字塔参考点初构建

DSO使用了最新关键帧作为跟踪过程中的参考关键帧。为了提高跟踪鲁棒性，滑动窗口中的所有激活地图点都会投影到最新关键帧的第0层上。正如下面这个图所描述的那样，来初始化跟踪参考关键帧上第0层的像素点逆深度。

在投影过程中，DSO系统使用了四舍五入的方式来计算投影点的像素位置，因此存在多个点投影到同一个像素位置的情况，这里使用DSO中的初始化的3.3节讲到的高斯归一化积解决同像素位置不同逆深度的问题。

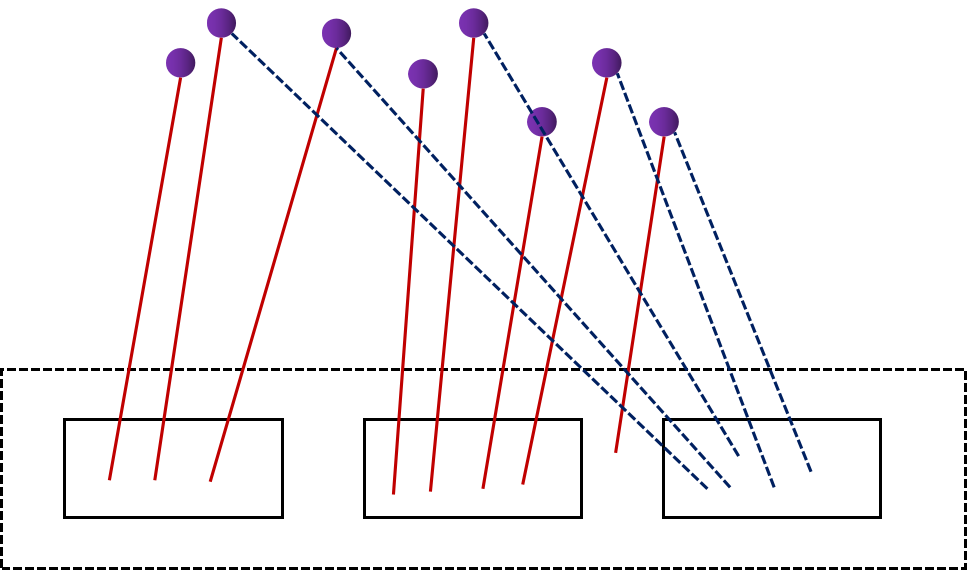
根据跟踪参考帧第0层上的像素逆深度点，向上层进行投影得到参考帧第1层的像素逆深度点，以此类推最终得到初步的跟踪参考点逆深度，这里同样会存在多对一的情况，依然使用高斯归一化积解决。

1.2 金字塔参考点膨胀

除了使用上述投影方式，DSO的源码中使用了膨胀手段来进一步增加参考点的数目，正如下图所示，紫色的位置代表某个金字塔层级上没有逆深度点的像素位置，而青色位置代表膨胀遍历位置，即遍历青色位置试图寻找一个有逆深度的像素点，然后使用取均值的方式再紫色位置膨胀出逆深度点出来。下图是DSO中采用的两种膨胀遍历方式，左侧是金字塔0层和1层的膨胀方式，右侧是其他层的膨胀方式。

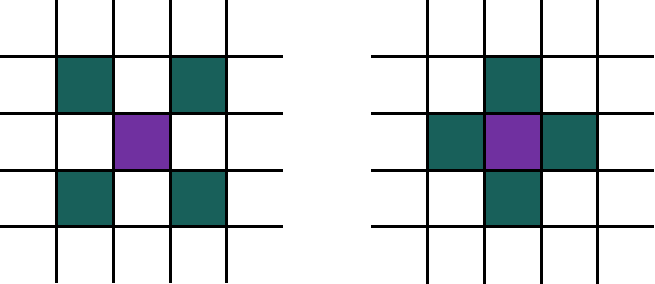
膨胀点原因猜测

这里膨胀点的方式和我在DSO中的优化模型文章中提到的pattern类似，pattern的作用是使用周围像素共享中心点的逆深度，以此来增强灰度不变形假设的可行性。个人猜测DSO在这里使用膨胀的原因和pattern类似，尝试以这种方式提高假设的可靠性。

2. 实施跟踪过程（构建模型并优化）

有了参考帧和待跟踪的参考点后，就可以实施前端跟踪过程了。除了使用图像金字塔从粗到精的跟踪手段外，DSO还拓展了不同的运动假设来构建优化初值假设库，试图找到一个最优初值，从而加速优化过程，提高达到最优值的可能性。

2.1 构建优化初值假设库

DSO考虑了恒速运动、倍数运动、半速运动和相对参考帧静止的模型假设，除此之外DSO还做了小旋转运行假设，所有的运动假设模型我都在下面的图片里面表示了出来，共有$(3 * 3 * 3 - 1) * 3 + 4$种假设结果。其中待优化帧的光度仿射参数$a_j$和$b_j$直接使用的上一帧光度仿射参数$a_{last}$和$b_{last}$作为初值，这是因为自然条件下，相邻帧之间的光度仿射参数变化非常小。

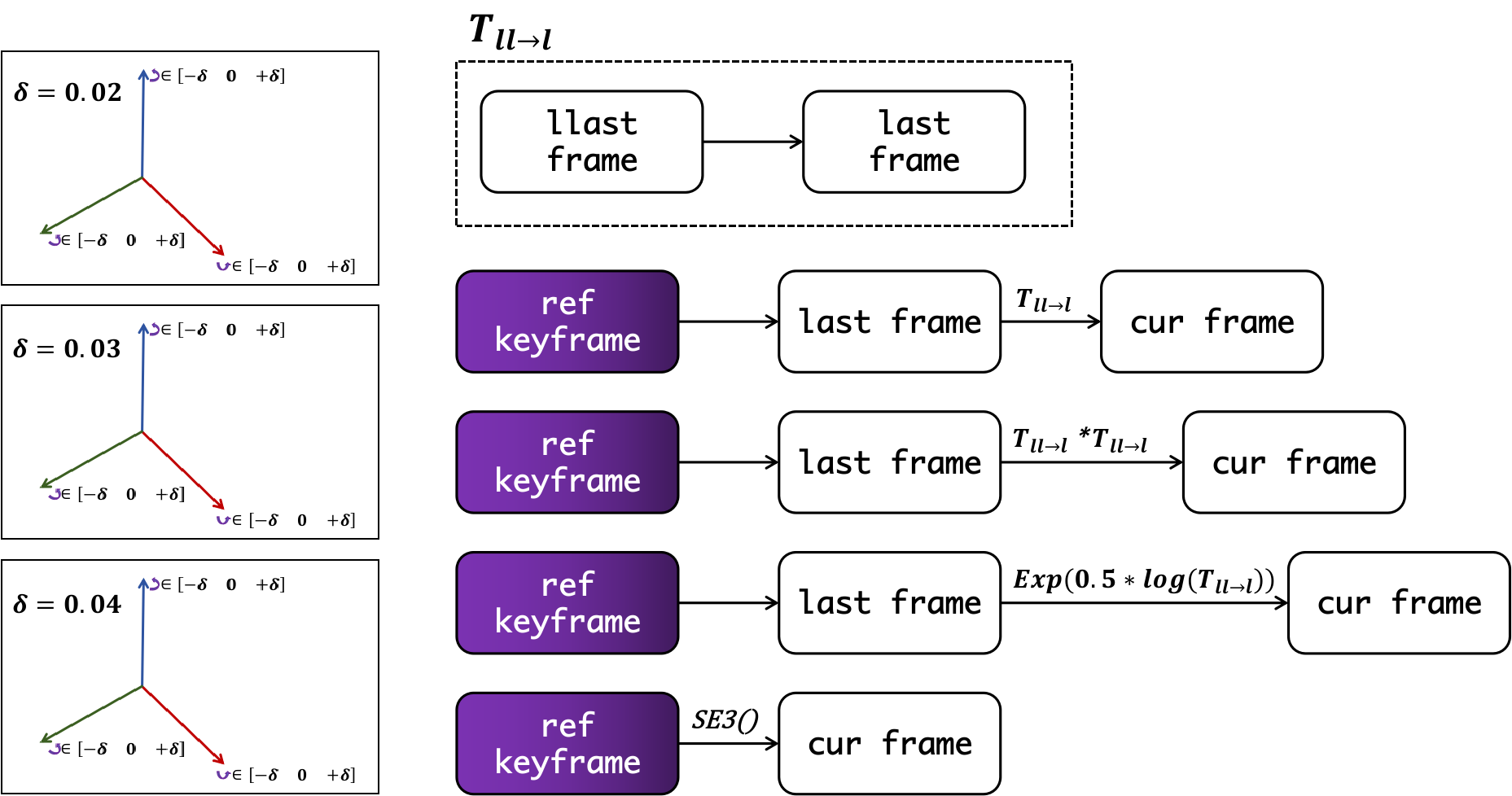
2.2 基于某种假设的跟踪尝试

2.2.1 跟踪模型

某种位姿假设初值$T_{cr}$确定后，DSO前端跟踪部分会使用下面的公式构造优化目标函数。

$$ E_{l}=\sum_{p_i \in ref}{||r_k||_{\gamma}} \\ r_k=I_j[p_j]-\frac{t_j e^{a_i}}{t_i e^{a_j}}I_i[p_i]-(b_j - \frac{t_j e^{a_i}}{t_i e^{a_j}} b_i) $$

其中：

$p_i$为跟踪参考关键帧ref frame$l$层上，带有逆深度的参考点。
$p_j$为使用当前优化参数投影到当前帧$l$层上的点。
$E_l$为$l$层金字塔上的能量值，同样也是优化目标函数。

与DSO中的优化模型文章中的模型对比发现，跟踪模型并没有使用pattern，这部分也印证了我在1.2小节中的猜测。

2.2.2 雅可比矩阵构建

虽然模型没有使用pattern，但是残差部分是一致的，因此雅可比矩阵的构建也完全一致。在前端位姿估计部分，不涉及地图点逆深度的优化问题，因此待优化量主要有当前帧相对于跟踪参考帧的位姿$T_{cr}$以及当前帧的光度仿射参数$a_j$和$b_j$，对于$a_j$和$b_j$来讲，它们的求导是平凡的，而相对位姿$T_{cr}$的求导，我在文章DSO中的优化模型中做了详细描述，这里只写出相关结论。

$$ \begin{align*} \frac{\partial{r_k}}{\partial{\xi_{ji}}}&= \frac{1}{P_Z'} \begin{bmatrix} d_x&d_y \end{bmatrix} \begin{bmatrix} f_x & 0 \\ 0 & f_y \end{bmatrix} \begin{bmatrix} 1 & 0 & -\frac{P_X'}{P_Z'} \\ 0 & 1 & -\frac{P_Y'}{P_Z'} \\ \end{bmatrix} \begin{bmatrix} d_{pi}&-P'^{\wedge} \end{bmatrix}\\ &= \begin{bmatrix} d_xf_x&d_yf_y\end{bmatrix} \begin{bmatrix} \frac{d_{pi}}{P_{Z}'} & 0 & -\frac{d_{pi}}{P_{Z}'}\frac{P_{X}'}{P_{Z}'} & -\frac{P_{X}'P_{Y}'}{P_{Z}'^2} & 1+\frac{P_{X}^{2}}{P_{Z}^{2}} & -\frac{P_{Y}'}{P_{Z}'} \\ 0 & \frac{d_{pi}}{P_{Z}'} & -\frac{d_{pi}}{P_{Z}'}\frac{P_{Y}'}{P_{Z}'} & -1-\frac{P_{Y}^{2}}{P_{Z}^{2}} & \frac{P_{X}'P_{Y}'}{P_{Z}^{2}} & \frac{P_{X}'}{P_{Z}'} \end{bmatrix}\\ \frac{\partial r_k}{\partial a_j}&=\frac{t_j e^{a_i}}{t_i e^{a_j}}(b_i-I_i[p_i])\\ \frac{\partial r_k}{\partial b_j}&=-1 \end{align*} $$

跟踪部分的细节性问题

计算残差时，采用动态阈值调节的手段，即先确定一个相对可控的残差阈值，然后根据内点比例适当地调整倍率来确保有足够的内点进行优化。当这个可控阈值调整过后，说明某层优化的残差相对较大，为了保证收敛，会对这一层进行再次优化。（调整过阈值的层会优化两次，怀疑内点比例低）
当某一层优化收敛后，会判断最终的优化RMSE和所有尝试的最小RMSE * 1.5做判断，如果大于1.5倍的最小值，则认定这次尝试直接失败，退出这次尝试，以节省时间，源码中维护这一行为的变量为achieveRes。
如何判断某次尝试失败与否？DSO从光度仿射参数的相对量和绝对量上判断是否优化成功，$a_j > 1.2$ 或者 $b_j > 200$则失败，$a_{ji}>1.5$或者$b_{ji}>200$则认为失败。
如何提前退出尝试？从2.1节的介绍中可以发现，一共有$(3 * 3 * 3 - 1) * 3 + 4 = 82$次尝试，DSO为了避免多次尝试导致的时间浪费问题，会使用上一帧优化能量值 * 1.5 作为退出尝试的条件，当然这样就可能导致动态阈值一直增大的情况。DSO在关键帧判断中对这个问题做了约束，保证了动态阈值增长的上限（见本章第3节）。

3. 关键帧判断（跟踪后处理）

在关键帧的判断中，除了通常考虑的时间间隔和空间间隔外，DSO还考虑了光度变化和用来提前退出尝试的跟踪能量阈值。

DSO中考虑的时间间隔相对普通，会人为限定一个创建关键帧的最大时间间隔，在DSO的源码中默认是不开启这个配置的。
DSO考虑的空间间隔相对新颖，不是所谓的真实距离，而是考虑了某些位姿间隔条件下的平均光流大小（金字塔第0层）。我们知道两张图像的平均光流大小可以近似的代表两张图像之间的视差，光流越大，视差越大，两张图片的重叠部分越少，反之亦然。DSO使用$T_{cr}$中的$t_{cr}$、$-t_{cr}$、$T_{cr}$和$[R_{cr},t_{cr}]$四种位姿导致的平均光流，配合自定义权重判断是否需要创建关键帧。使用四种位姿的平均光流而不是仅仅$T_{cr}$造成的平均光流，我猜测可能是因为使用四种位姿可以在一定程度上模拟之后一段时间内的运动状态，从而做到提前判断。
DSO使用了基于光度仿射参数的直接法，因此当相对仿射参数$a_{ji}$变化较大时，代表着当前帧和参考关键帧之间的光照条件发生了相对较大的变化，因此需要及时创建关键帧防止跟踪丢失情况的发生。
在第2小节的末尾，做了一些跟踪细节方面的讨论，提到了提前退出尝试的动态阈值可能会持续增大，从而导致阈值限定意义失效，DSO为了防止这种情况的发生，会提前记录基于当前参考关键帧第一次跟踪成功的能量值，如果当前帧跟踪阈值超过了这个值的2倍，则认定需要创建关键帧了，这么做相当于对动态阈值的上限做了规定。

孙善路-github 对SLAM和DL感兴趣的理工男

孙善路-bilibili 对SLAM和DL感兴趣的理工男

有什么问题吗，有任何问题欢迎你在下面评论留言或者邮件联系我！

Comments