DSO后端建图（滑窗优化）

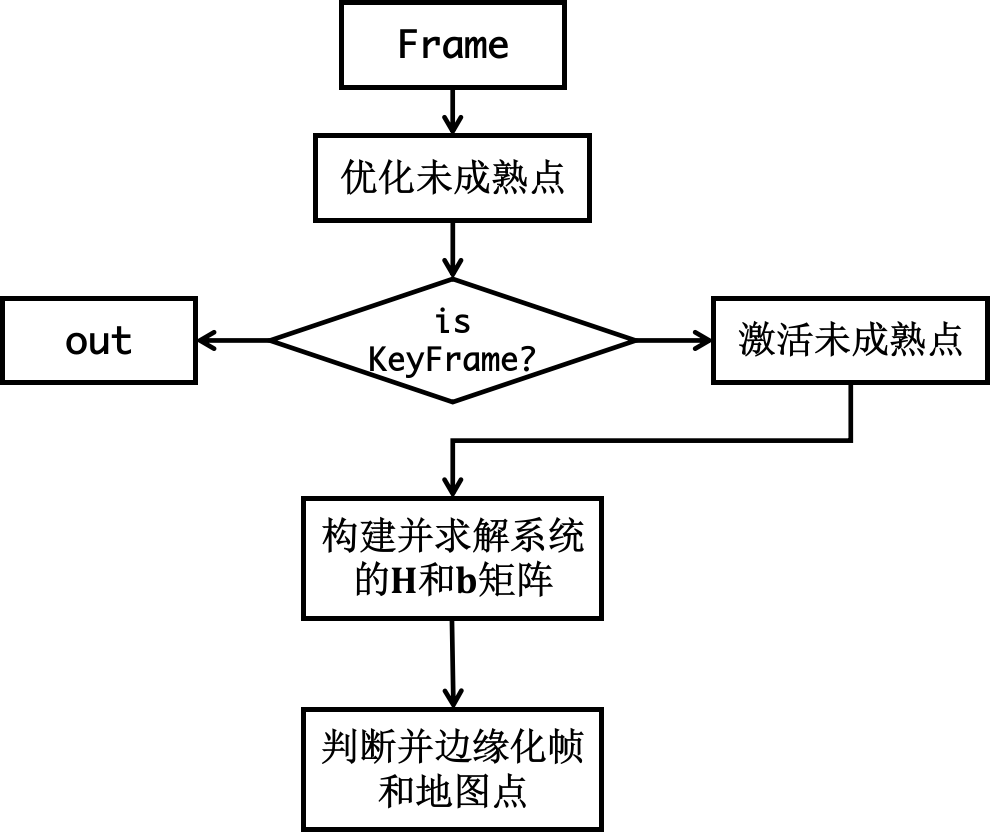
当前端跟踪完成后，前端线程会判断是否需要添加关键帧操作，并向后端发送跟踪完成的当前帧，如果不需要添加关键帧，那么可以根据当前帧的位姿信息对滑窗中的未成熟点进行优化更新；当然如果需要添加关键帧的话也需要根据位姿信息对滑窗中的未成熟点进行优化更新，除此之外还需要根据当前滑窗中的状态激活相当一部分的未成熟点ImmaturePoint，然后根据滑窗中的成熟点PointHessian、关键帧、先验信息以及由系统之前边缘化marg的fill-in信息构建最小二乘的图优化问题，当然这里会涉及到一些优化理论知识，比如：

DSO使用First Estimate Jacobian FEJ，解决由于不同优化初值导致的系统不一致性问题。
DSO使用 SVD分解 求正规方程或者使用向零空间投影的方式求解最小二乘问题，来防止解在零空间中漂移的问题。
DSO使用矩阵伴随的性质，构建$\frac{\partial \delta \xi_{ji}}{\partial \delta \xi_j}$和$\frac{\partial \delta \xi_{ji}}{\partial \delta \xi_i}$以此来解决相对增量到绝对增量的转换问题（这是由于残差定义仅包含相对位姿导致的问题）。

最后，DSO定义了一些高效的帧管理和点管理策略，使用某些条件筛选需要被边缘化掉的帧和点，以此构建滑动窗口的边缘化信息HM和bM。

1. 滑窗优化里面到底在做什么？

首先，当前端线程完成对Frame的位姿估计后，需要后端线程根据估计的Frame位姿进行滑动窗口中未成熟点ImmaturePoint的逆深度更新，具体更新逆深度的手段，我会在第2小节中进行说明。如果前端线程判断滑动窗口中不需要添加关键帧，那么后端线程结束；否则，后端线程进入滑动窗口优化阶段。为了保证滑窗中激活点PointHessian 的密度问题，需要对滑动窗口中作为备选力量的未成熟点ImmaturePoint 进行筛选激活，而筛选激活的策略，我会在第3小节中进行说明。当滑动窗口中激活点达到数量要求后，构建残差（根据DSO中的优化模型文章描述的残差公式构建），然后在考虑残差作用、先验作用、marg作用后构建并迭代求解优化的正规方程H和b，滑窗正规方程的构建过程以及构建求解过程中可能出现的问题，我会在第4小节中进行详细描述；最后为了保证求解的实时性，需要严格控制滑动窗口中的规模，DSO使用边缘化的策略来实现，其中会涉及边缘化判断和实施边缘化操作这两个过程来构建边缘化的$H_M$和$b_M$，以供后续滑窗优化使用，我会在第5小节中对边缘化相关内容进行详细描述。整个后端的运行逻辑如下图所示：

2 普通帧和关键帧都要做的未成熟点优化

DSO中的未成熟点优化过程分两个步骤进行，首先需要通过未成熟点的逆深度范围确定的极线线段上搜索一个能量最小的像素点；接下来根据线搜过程以及残差公式构建优化模型，因为残差和待优化量都是标量，因此优化过程可以非常快，整个未成熟点优化过程如下图所示：

2.1 极线搜索

DSO中的极线搜索与视觉SLAM十四讲p309中讲解极线搜索内容基本一致，只不过是块匹配策略不一致而已，在SLAM十四讲中列举了SAD、SSD和NCC块匹配评价方法，而DSO使用的是其pattern根据残差构建能量值来作为极线搜索的块匹配评价方法，DSO使用构建残差能量值的方式也会为基于极线搜索优化过程提供方便。

DSO极线搜索中的小问题

pattern 在线搜过程如何保证？在SLAM十四讲中，提到了块匹配技术，也就是说以投影点和被投影点为中心，与周围的某些固定点之间构建两个图像块，以此来进行极线搜索过程中的匹配区域。但是DSO有固定的pattern，但是根据投影公式分析可知$p_j=KRK^{-1}p_i + Ktd_{pi}$，在搜索过程中，$d_{pi}$是未知的，所以投影点$p_i$和被投影点$p_j$没有明确的pattern对应。DSO使用了$KRK^{-1}$矩阵的左上$2\times2$矩阵和pattern相对量的乘积来近似代表pattern与$p_j$点的相对位置。
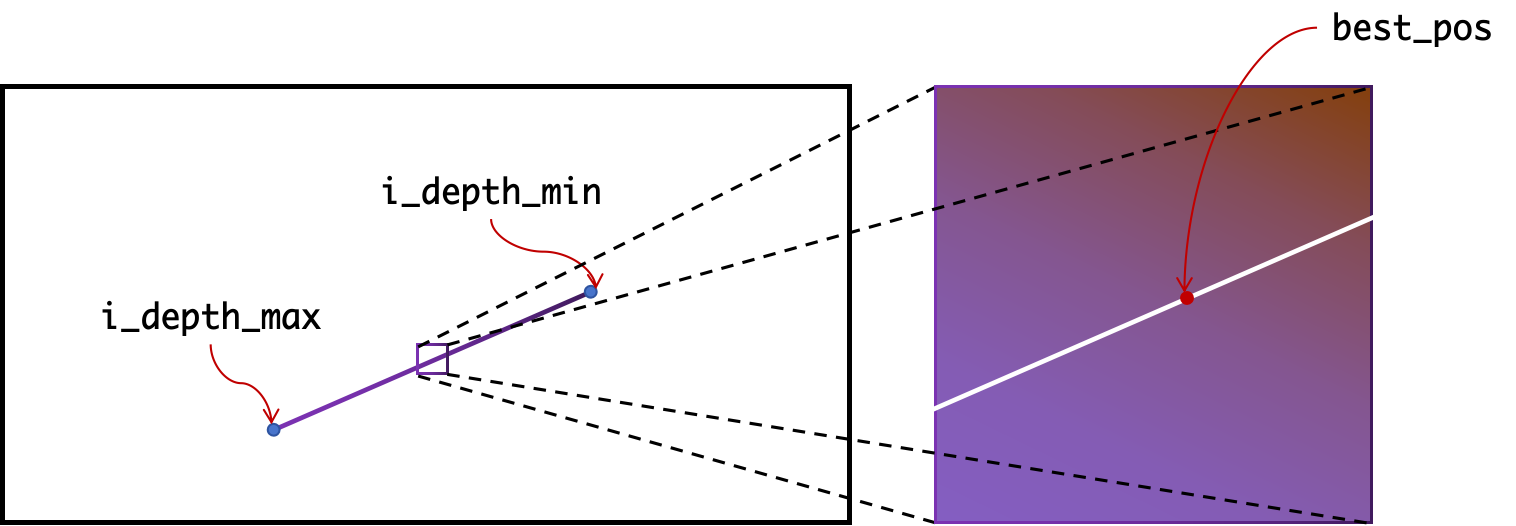
线搜起止点如何确定？DSO使用了未成熟点的idepth_min 和 idepth_max 对应的点作为搜索的起止点，当然idepth_min被初始化为0，idepth_max被初始化为NAN，如果idepth_max为NAN,则通过图像的(width + height) * super_param来确定一个搜索长度。

除此之外，DSO还讨论了极线搜索和梯度的关系，我在网络上找到了相关的解释，根据下面的图像进行分析，图中红色实线代表的是根据当前帧位姿得到的极线，而红色虚线代表真实位姿得到的极线，蓝色的线代表的是像素值等值线（垂直于像素梯度），这里假设虚线上浅蓝色点为真实的匹配点，而实线上浅蓝色点是在误差极线上搜索到的匹配点。

左图是极线和梯度平行时，可能会导致的像素误差。可以发现，总体的像素误差主要由极线误差导致。
右图是极线和梯度之间存在角度差时，可能会导致的像素误差，可以发现，整体像素误差除了有一部分来自极线误差外，还有一部分来自梯度的误差。

DSO源码中使用了一个经验公式，来计算像素误差的大小，经验公式如下：

$$ e_p = 0.2 + 0.2 \times \frac{a + b}{a}\\ a = (lx \times dx + ly \times dy)^2\\ b = (lx \times dx - ly \times dy)^2 $$

其中：

$lx$为极线在$x$方向上的分量
$ly$为极线在$y$方向上的分量
$dx$为梯度在$x$方向上的向量
$dy$为梯度在$y$方向上的向量

经过推导不难发现，$e_p=0.2 + \frac{0.2}{\cos^2<l,d>}$，其中$cos<l,d>$为极线与梯度之间的夹角的余弦值，也就是说极线和梯度之间的夹角越大就会导致像素误差越大，并且最小的像素误差为0.4px。这与我在上面的定性分析结果一致。

极线搜索与梯度关系，定性分析存在的问题

位姿误差是如何影响极线的呢？在图像上看来，误差极线和真实极线之间是平行的。通过视觉SLAM十四讲中的推导可以知道，极线搜索的线段参数可以使用$Fp_1$来表示，其中F为基础矩阵，$p_1$为host帧上的像素点。而$F$矩阵可以使用$F=K^{-T}t^{\wedge}RK^{-1}$表示，我从这个公式上很难判断出位姿误差会导致平行的极线误差。
以真实匹配点为起点的图像等值线与误差极线的交点是否能保证与误差极线上搜索的点一致？我认为在极线误差较小的情况下，这个是可以成立的，因为真实匹配点能近似代表误差最小点处，而图像等值线在较小的像素范围内可以看做近似成立，因此误差极线上的点也能近似代表误差最小点处。

2.2 基于极线搜索优化

线搜结束后，可以得到一个粗略的最优值（因为线搜会有步长，以至于找不到全局最优值），因此需要优化过程来逼近极线上的最优值对应的$p_j$点。线搜过程和残差可以通过下面的公式进行表示：

$$ r_k=I_j[p_j]- a_{ji} I_i[p_i] - b_{ji}\\ p_j=l*\delta + p_{j0} $$

其中：

$p_j$为极线搜索的目标点；
$l$为极线方向；
$p_{j0}$为极线搜索结束后确定的$p_j$点；
$\delta$为极线上最优点的$p_j$到当前$p_{j0}$之间的步长（待优化量）；

那么不难推导，残差相对步长$\delta$的雅可比矩阵如下：

$$ \frac{\partial r_k}{\partial \delta}=g^T l $$

其中：

$g$为$p_j$点的梯度值；
$l$为极线方向；

使用GN或者LM方法优化完成后，考虑最优化后的线搜点$p_j=[u,v]^T$，由具体的投影公式推导可以得到逆深度点：

$$ p_r = KR_{ji}K^{-1}[p_i^T, 1]^T\\ {d_{pi}}_u=\frac{p_r[2]\times u - p_r[0]}{Kt_{ji}[0]-Kt_{ji}[2]\times u}\\ {d_{pi}}_v=\frac{p_r[2]\times v - p_r[1]}{Kt_{ji}[1]-Kt_{ji}[2]\times v} $$

除此之外，DSO还需要考虑由于极线误差和像素梯度造成的像素误差errorPixel造成逆深度不确定性的影响，得到逆深度点的min和max如下：

$$ {{d_{pi}}_u}_{min}=\frac{p_r[2]\times (u - l_x\times e_p) - p_r[0]}{Kt_{ji}[0]-Kt_{ji}[2]\times (u - l_x \times e_p)}\\ {{d_{pi}}_v}_{min}=\frac{p_r[2]\times (v - l_y\times e_p) - p_r[1]}{Kt_{ji}[1]-Kt_{ji}[2]\times (v - l_y\times e_p)}\\ {{d_{pi}}_u}_{max}=\frac{p_r[2]\times (u + l_x\times e_p) - p_r[0]}{Kt_{ji}[0]-Kt_{ji}[2]\times (u + l_x \times e_p)}\\ {{d_{pi}}_v}_{max}=\frac{p_r[2]\times (v + l_y\times e_p) - p_r[1]}{Kt_{ji}[1]-Kt_{ji}[2]\times (v + l_y\times e_p)} $$

其中：

$u$为$p_j$的x坐标值；
$v$为$p_j$的y坐标值；
$e_p$为由经验公式求得的像素误差；
$l_x$为单位极线方向的x值；
$l_y$为单位极线方向的y值；
最后，从两个min值和两个max值中选择一个最小值和一个最大值来更新未激活点的idepth_min和idepth_max即可。

3 未成熟点如何激活？

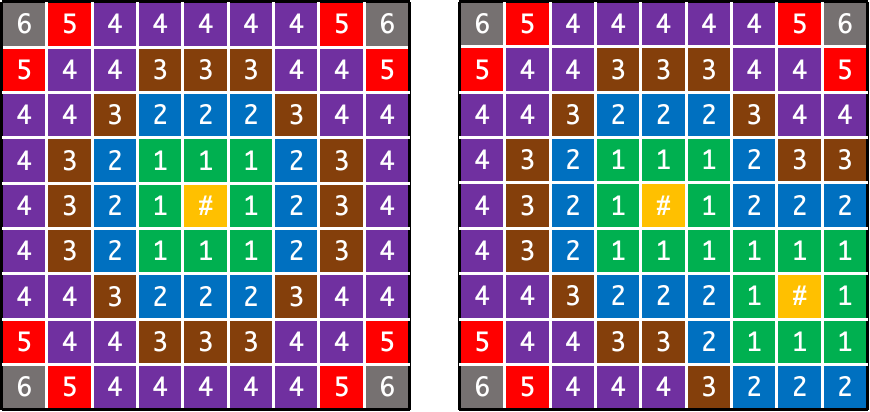
未成熟点激活部分主要涵盖三方面的内容：构建距离地图，激活条件判断、激活点逆深度值优化。以最新关键帧kf的金字塔第一层作为滑窗中现存激活点的投影位置。当某一个激活点投影到kf的第一层后，更新相对像素距离到距离地图上。我想下面的图里描述的应该非常清楚（#代表的是滑窗中的激活点投影位置），值得注意的是，针对某个投影点进行距离地图更新时，需要考虑其他投影点的位置，即某个像素位置A距离投影点p1的位置为5，而计算出距离另一个投影点为4时，就需要更新距离地图上的A位置为4，而不是5。

激活条件的判断主要考虑了下面四种情况：

未成熟点在最新的极线搜索中，它的线搜距离在8个像素以内，代表逆深度值达到一个收敛的范围；
未成熟点在最新的极线搜索中，要求搜索点的质量quality大于3，质量被定义为次优线搜能量值 / 最优线搜能量值；
要求未成熟点的逆深度平均值（idepth_min + idepth_max）大于0；
要求未成熟点可以投影到最新关键帧上，并且要满足距离地图的约束（DSO源码里面做了动态阈值调整，应该是根据工程实践调整出来的超参数）；

对于那些被判断为可以激活的点，DSO将其分别投影到滑动窗口中的关键帧上，构建正规方程，并进行优化迭代求解，其残差构建和雅可比矩阵的求解我在DSO中的优化模型文章中做了详细的推导，这里直接写结论：

$$ r_k = I_j[p_j] - a_{ji}I_i[p_i] - b_{ji}\\ \begin{align*} \frac{\partial{r_k}}{\partial{d_{pi}}}&= \frac{1}{P_Z'} \begin{bmatrix} d_x&d_y \end{bmatrix} \begin{bmatrix} f_x & 0 \\ 0 & f_y \end{bmatrix} \begin{bmatrix} 1 & 0 & -\frac{P_X'}{P_Z'} \\ 0 & 1 & -\frac{P_Y'}{P_Z'} \\ \end{bmatrix} \begin{bmatrix} t_{ji}^X\\t_{ji}^Y\\t_{ji}^Z \end{bmatrix}\\ &= \frac{1}{P_Z'}[d_xf_x(t_X^{ji}-\frac{P_X'}{P_Z'}t^Z_{ji})+d_yf_y(t_Y^{ji}-\frac{P_Y'}{P_Z'}t^Z_{ji})] \end{align*}\\ H_{dd}=\sum_{j\in \Omega}^{j!=i}{\sum_{p_i \in \mathcal{N(p)}}{\frac{\partial{r_k}}{\partial{d_{pi}}}^T\frac{\partial{r_k}}{\partial{d_{pi}}}}}\\ b_d=\sum_{j\in \Omega}^{j\neq i}{\sum_{p_i \in \mathcal{N(p)}}{\frac{\partial{r_k}}{\partial{d_{pi}}}^Tr_k}} $$

其中：

$\Omega$为滑动窗口中的关键帧索引集合；
$i$为$p_i$点对应的host帧索引；
$j$为$p_i$点投影的target帧索引；
$\mathcal{N(p)}$代表的是以$p$为中心的pattern。

从残差对$p_i$点逆深度的雅可比矩阵来看，其优化过程应该相当迅速，因为正规方程中涉及到的内容全是标量。

4 如何根据关键帧和路标点构建优化的正规方程？

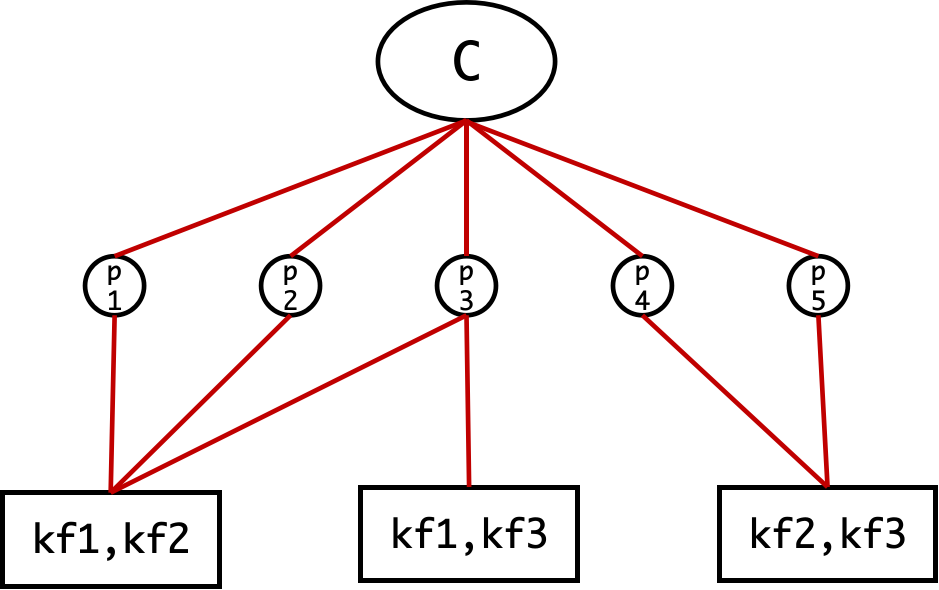
这里我们假设地图点激活后，滑动窗口中有3个关键帧和5个地图点，上图表示了帧与帧之间的可视关系，以及帧与激活点之间的可视关系。其中红色线代表某个点的host帧，黑色线代表着某个帧可以看到某个点。

根据DSO中的优化模型文章中的残差模型推导，后端的优化能量函数，残差公式和残差的雅可比矩阵如下：

$$ E_{fpC}=\sum_{i\in \Omega, j \in \Omega}^{j \neq i} \sum_{p \in C(I_i)}\sum_{p_i \in \mathcal{N(p)}} {||r_k||_{\gamma}}\\ r_k=I_j[p_j]-\frac{t_je^{a_i}}{t_ie^{a_j}}I_i[p_i]-(b_j-\frac{t_je^{a_i}}{t_ie^{a_j}}b_i)\\ \frac{\partial{r_k}}{\partial{d_{pi}}}= \frac{1}{P_Z'}[d_xf_x(t_X^{ji}-\frac{P_X'}{P_Z'}t^Z_{ji})+d_yf_y(t_Y^{ji}-\frac{P_Y'}{P_Z'}t^Z_{ji})]\\ \frac{\partial{r_k}}{\partial{\xi_{ji}}}= \begin{bmatrix} d_xf_x&d_yf_y\end{bmatrix} \begin{bmatrix} \frac{d_{pi}}{P_{Z}'} & 0 & -\frac{d_{pi}}{P_{Z}'}\frac{P_{X}'}{P_{Z}'} & -\frac{P_{X}'P_{Y}'}{P_{Z}'^2} & 1+\frac{P_{X}^{2}}{P_{Z}^{2}} & -\frac{P_{Y}'}{P_{Z}'} \\ 0 & \frac{d_{pi}}{P_{Z}'} & -\frac{d_{pi}}{P_{Z}'}\frac{P_{Y}'}{P_{Z}'} & -1-\frac{P_{Y}^{2}}{P_{Z}^{2}} & \frac{P_{X}'P_{Y}'}{P_{Z}^{2}} & \frac{P_{X}'}{P_{Z}'} \end{bmatrix}\\ \frac{\partial r_k}{\partial a_{ji}}=-(I_i[p_i]-b_i)\\ \frac{\partial r_k}{\partial b_{ji}}=-1 $$

其中：

$E_{fpC}$为所有残差组成的能量部分，每个残差都由三个顶点组成，分别是$ij$帧之间的相对参数、点$p$的逆深度$d_{pi}$和相机内参$C$，因为DSO的相机内参是由算法计算出来的，因此需要进行在线标定内参，我在DSO中的去畸变操作中详细描述了DSO相机内参的计算过程；
后端滑窗中使用的$a_{ji}=\frac{t_je^a_{i}}{t_ie^{a_j}}$，与初始化过程的$a_{ji}$不同，初始化过程中是为了保证$e^{a_{ji}}>0$，而后端部分不需要这个保证，因为$a_{ji}$的计算只是做一个雅可比中转的作用，并且使用这种中转方式可以简化整个雅可比的推导过程（相比使用$e^{a_ji}$作为中间量）；
$\frac{\partial r_k}{\partial d_{pi}}$和$\frac{\partial r_k}{\partial \delta \xi_{ji}}$部分直接使用的我在DSO中的优化模型文章中推导的结论；
残差对仿射参数的求导相对简单，都是通过$a_{ji}=\frac{t_je^{a_{i}}}{t_ie^{a_{j}}}$和$b_{ji}=b_j - a_{ji} b_i$作为中间变量进行推导即可，整个推导过程比较简单，这里就不展开说明了；

由于DSO使用算法的方式计算出了一个虚拟的相机内参，因此DSO对相机内参做了在线标定，在滑窗优化过程中，将相机内参作为优化变量，求解残差对相机内参的雅可比矩阵，这个推导过程比较繁琐，涉及正向投影和反向投影两个部分，下面对残差相对内参的雅可比矩阵的详细推导：

反向投影过程，代表$p_i$点向$i$帧的归一化坐标系上进行反向投影：

$$ X_i^n=\frac{1}{f_x}u_i-\frac{c_x}{f_x}\\ Y_i^n=\frac{1}{f_y}v_i-\frac{c_y}{f_y}\\ \frac{\partial P_i^n}{\partial C}=\begin{bmatrix} -\frac{u_i}{f_x^2} & 0 & -\frac{1}{f_x} & 0 \\ 0 & -\frac{v_i}{f_y^2} & 0 & -\frac{1}{f_y} \\ 0 & 0 & 0 & 0 \end{bmatrix} $$

正向投影过程，代表由$i$帧归一化坐标系$P_i^{n}$向$j$帧像素坐标系的投影过程，包含一个坐标变换和投影过程：

$$ P_j' = R_{ji}P_i^{n}+t_{ji}d_{p_i}\\ u_j = f_x \frac{X_j'}{Z_j'} + c_x\\ v_j = f_y \frac{Y_j'}{Z_j'} + c_y\\ \frac{\partial p_j}{\partial C} = \begin{bmatrix} \frac{X_j'}{Z_j'} & 0 & 1 & 0 \\ 0 & \frac{Y_j'}{Z_j'} & 0 & 1 \end{bmatrix}\\ \frac{\partial p_j}{\partial P_i^n}=\frac{\partial p_j}{\partial P_j'} \times \frac{\partial P_j'}{\partial P_i^n}=\begin{bmatrix} \frac{f_x}{Z_j'} & 0 & -\frac{f_xX_j'}{Z_j'^2}\\ 0 & \frac{f_y}{Z_j'} & -\frac{f_yY_j'}{Z_j'^2} \end{bmatrix}\times R_{ji} $$

结合正向和反向投影过程，可得残差对相机内参$C$的雅可比矩阵：

$$ \begin{align*} \frac{\partial r_k[p_j(C,P_i^n(C))]}{\partial C} &= \frac{\partial r_k}{\partial p_j}\times (\frac{\partial p_j}{\partial C} + \frac{\partial p_j}{\partial P_i^n}\times \frac{\partial P_i^n}{\partial C})\\ &=\begin{bmatrix}d_x & d_y\end{bmatrix} ( \begin{bmatrix} \frac{X_j'}{Z_j'} & 0 & 1 & 0 \\ 0 & \frac{Y_j'}{Z_j'} & 0 & 1 \end{bmatrix}+ \begin{bmatrix} \frac{f_x}{Z_j'} & 0 & -\frac{f_xX_j'}{Z_j'^2}\\ 0 & \frac{f_y}{Z_j'} & -\frac{f_yY_j'}{Z_j'^2} \end{bmatrix}\times R_{ji}\times \begin{bmatrix} -\frac{u_i}{f_x^2} & 0 & -\frac{1}{f_x} & 0 \\ 0 & -\frac{v_i}{f_y^2} & 0 & -\frac{1}{f_y} \\ 0 & 0 & 0 & 0 \end{bmatrix} ) \end{align*} $$

根据DSO的残差模型，可以绘制图优化的优化图如下图所示，其中红色线连接三个顶点，分别为两帧之间的相对量顶点和激活点逆深度顶点和相机内参顶点。

根据上图所示的优化图，可以绘制由这些残差构建的Hessian矩阵如下图所示，但是这里会出现一些问题，如果去解这一个由两帧相对量和激活点构建的Hessian矩阵的话，得到的结果应该都是相对量增量，这样解出来的结果只是求解出了滑动窗口帧之间的相对量Tth、a_th和b_th，而不是相对于世界坐标系的绝对量。

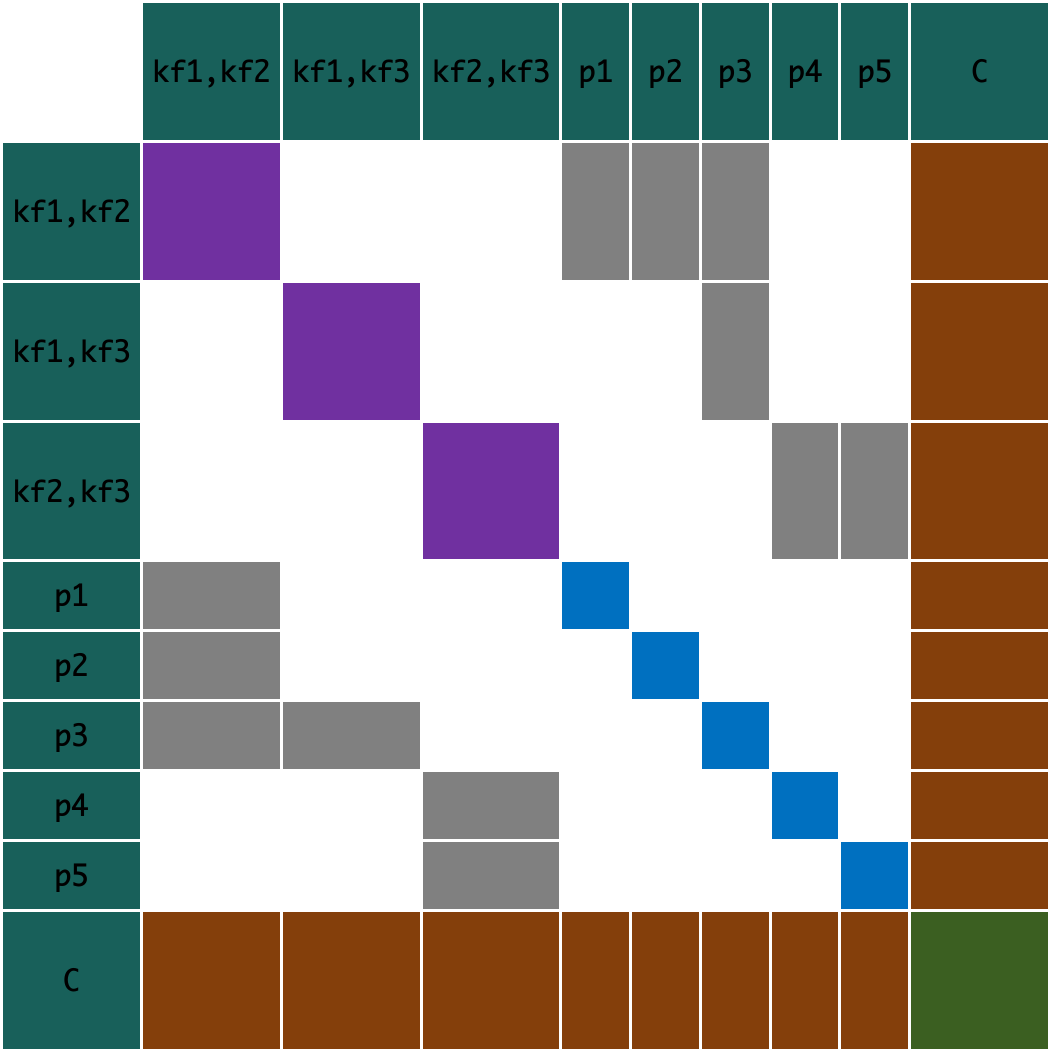
讨论仅求帧相对量的可行性

我认为，仅求帧相对量不可行，我主要是通过一下三个方面来考虑的。

相对量求解完成后，需要更新为绝对量，也就是相对于世界坐标系的参数量，在更新绝对量过程中会出现冲突问题，假设有三个关键帧，那么相对位姿就会有T12、T13和T23三个，假设Tw1已知的情况下,Tw3可以通过两种方式表示，分别是Tw1 * T13和Tw1 * T12 * T23。这两种表示方法势必会产生冲突，这个冲突问题怎么解决呢？
就算可以通过某种方式，解决1中说明的更新冲突问题，那么当滑动窗口优化达到某个规模上限后，为了实时性势必会进行激活点和关键帧的边缘化操作，假设系统判定，当前需要边缘化$f_1$这个关键帧，对于绝对量的表示来讲，其边缘化所表达的概率模型为 $p(f_1,f_2,f_3,p_1,p_2,p_3,p_4,p_5)=p(f_2,f_3,p_1,p_2,p_3,p_4,p_5|f_1) * p(f_1)$，其中边缘化完成后$p(f_1)$为常量概率。但是对相对量来讲，如何进行边缘化操作呢？不能把$f_1$涉及的所有相对量都进行边缘化吧，这样的话肯定会造成信息丢失。
最后，即便不考虑相对量边缘化操作造成的信息丢失，在求解正规方程上，相对量的Hessian矩阵的规模也要比绝对量表示的Hessian矩阵大得多。因为$C_n^2 \geq n,n\geq 2$总是成立的。因此使用schur分解加速正规方程求解时，相对量表示的分解后得到的稠密矩阵H，要比绝对量表示的稠密矩阵H大得多。

从上面三方面的分析来看，从可行性，信息留存率和效率三方面来讲，绝对量表示的正规方程都优于相对量表示的正规方程。

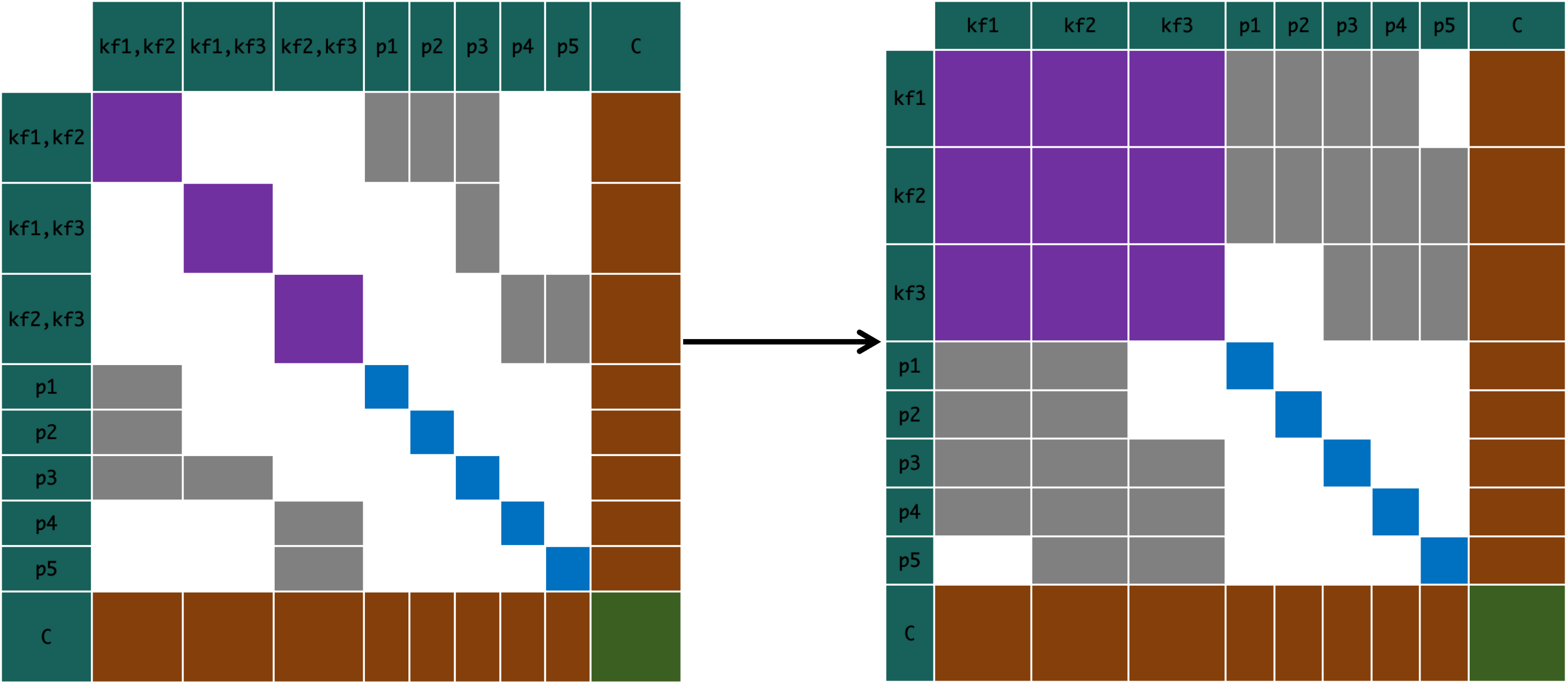
4.1 残差构建仅包含关键帧的相对量，怎么办？

从上面的分析中可知，绝对量表示的正规方程要优于相对量表示的正规方程，DSO使用位姿伴随的性质，求解$\frac{\delta\xi_{ji}}{\delta\xi_{i}}$和$\frac{\delta \xi_{ji}}{\delta \xi_{j}}$实现位姿相对量到绝对量的变换。而仿射参数的$\frac{\partial a_{ji}}{\partial a_i}$、$\frac{\partial a_{ji}}{\partial a_j}$、$\frac{\partial b_{ji}}{\partial b_i}$、$\frac{\partial b_{ji}}{\partial b_j}$可以根据残差方程直接推导出来，下面是推导流程。

首先，需要说明一个位姿矩阵的伴随性质，$Exp(Ad_T \times \xi)=TExp(\xi)T^{-1}$，其中$Ad_T$为位姿矩阵$T$的伴随矩阵，$\xi$为一个李代数上的小扰动。现在，考虑一个相对量位姿$T_{ji}$的左扰动$\delta \xi_{ji}$，它势必会造成$T_{jw}$和$T_{iw}$的小的左扰动，假设它们分别是$\delta \xi_j$和$\delta \xi_i$，它们的公式描述如下：

$$ \begin{align*} Exp(\delta \xi_{ji})T_{ji}&=Exp(\delta \xi_j) T_{jw} T_{iw}^{-1} \\ &\to Exp(\delta \xi_{ji})=Exp(\delta \xi_j) \to \frac{ \partial \delta \xi_{ji}}{\partial \delta \xi_j}=I\\ Exp(\delta \xi_{ji})T_{ji}&=T_{jw} (Exp(\delta \xi_i)T_{iw})^{-1}=T_{jw}T_{iw}^{-1}Exp(-\delta \xi_i)\\ &\to Exp(\delta \xi_{ji})=T_{ji}Exp(-\delta \xi_i)T_{ji}^{-1}=-Ad_{T_{ji}} \times \delta \xi_i \to \frac{ \partial \delta \xi_{ji}}{\partial \delta \xi_i}=-Ad_{T_{ji}} \end{align*} $$

相对仿射参数到绝对仿射参数之间的转换比较简单，可以根据残差公式直接推导：

$$ r_k=I_j[p_j]-\frac{t_je^{a_i}}{t_ie^{a_j}}I_i[p_i]-(b_j-\frac{t_je^{a_i}}{t_ie^{a_j}}b_i)\\ a_{ji}=\frac{t_je^{a_i}}{t_ie^{a_j}} \quad b_{ji}=(b_j-\frac{t_je^{a_i}}{t_ie^{a_j}}b_i)\\ \frac{\partial a_{ji}}{\partial a_i}=\frac{t_je^{a_j}}{t_ie^{a_i}}\\ \frac{\partial a_{ji}}{\partial a_j} = -\frac{t_je^{a_j}}{t_ie^{a_i}} \\ \frac{\partial b_{ji}}{\partial b_i}=-\frac{t_je^{a_j}}{t_ie^{a_i}}\\ \frac{\partial b_{ji}}{\partial b_j}= 1\\ $$

上面通过推导的形式，构建了$\frac{\partial \delta \xi_{ji}}{\partial \xi_j}$、$\frac{\partial \delta \xi_{ji}}{\partial \xi_i}$、$\frac{\partial a_{ji}}{\partial a_i}$、$\frac{\partial a_{ji}}{\partial a_j}$、$\frac{\partial b_{ji}}{\partial b_i}$、$\frac{\partial b_{ji}}{\partial b_j}$，因此可以计算残差相对于绝对量的雅可比矩阵，也就能完成基于相对量的Hessian矩阵到绝对量Hessian矩阵的转换。

4.2 为什么会有不一致性问题，该怎么解决？

DSO的后端使用的是滑动窗口的优化策略，因此DSO使用边缘化策略来控制整个后端滑动窗口中的规模。当然这个边缘化的操作是在后端优化完成后做的，其详细的策略我会在第5小节中描述，这里我们只需要知道，每次进行后端的滑动窗口优化时，都需要考虑最新边缘化操作得到的HM和bM矩阵。这代表着边缘化后剩余的信息，以最大似然估计的角度看，HM和bM中的信息代表着系统的条件概率，由于HM和bM会提供一个边缘化先验信息，它们所表达的约束为$H_M \delta x = -b_M$，这个约束可以为后续的优化操作提供方向。

与想象中不同的是，我们不能以下面这种方式使用边缘化得到的$H_M$和$b_M$：

$$ (H_A + H_M + H_P) \delta x = -(b_A + b_M + b_P) $$

其中：

$H_A$，$b_A$代表由滑动窗口中所有残差构建的H矩阵和b矩阵；
$H_M$，$b_M$代表边缘化后得到的H矩阵和b矩阵；
$H_P$，$b_P$代表先验信息的H矩阵和b矩阵；

不能直接进行相加的原因主要有两点，首先$H_A$和$H_M$线性化点的位置不同，这样直接相加会导致系统出现不一致性问题，其次$b_M$在优化中代表的是能量在线性化点$x_M$处的能量梯度（能量对待优化量的雅可比矩阵，在线性化点$x_M$处），但是随着更新的进行，两个线性化点$x_A$和$x_M$的距离可能逐渐变大，这样$b_M$就不能近似$x_A$处的能量梯度了，其中$x_A$代表的是残差的线性化点，$x_M$代表的是边缘化信息的线性化点，值得注意的是，$x_A$随着优化的进行，会逐渐改变，而$x_M$则不能改变。

对不一致性问题的详细说明：在论文 [1] 中，作者讨论了不同线性化点处的H矩阵直接相加导致了$H$矩阵的秩增加的情况（系统的某些状态由不客观变得可观了），也就是说这种不正确的操作低估了系统状态的不确定性，认定这种改变系统状态不确定性的问题为系统不一致性问题。下图清晰也表述了系统的不一致性问题，图中表示，系统的解为$xy=1$，具有一个状态是不可观的。如果将$E_1$在$x=0.5$处线性化，$E_2$在$x=1.2$处线性化后求解，导致系统的解坍缩成了一个点，从而失去了系统的不确定性。

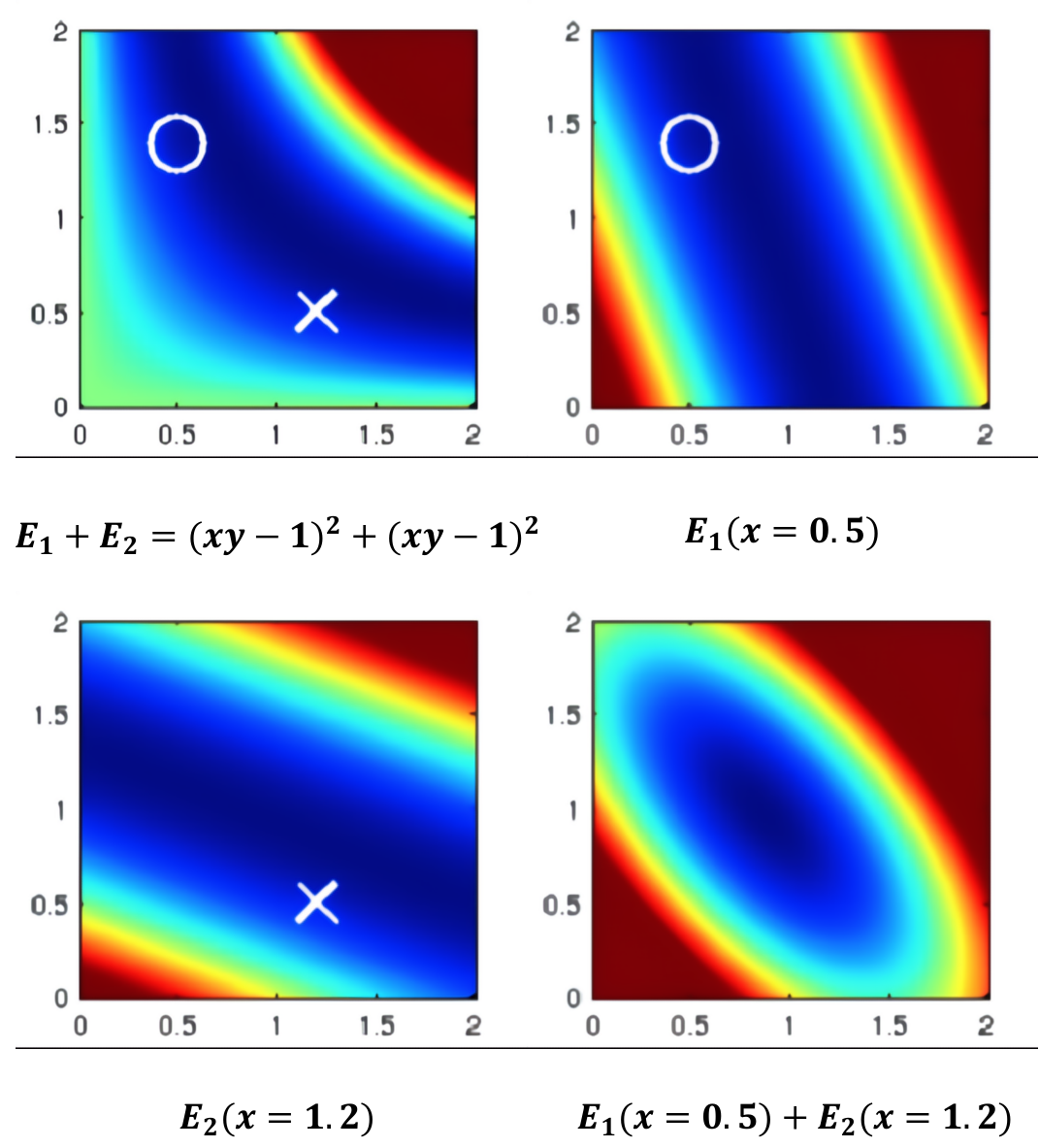
DSO使用了FEJ（First Estimate Jacobian）来解决不同线性化点导致的问题，FEJ是这样描述的，由于边缘化提供的$H_M$和$b_M$线性化点不能改变了，但是由线性化残差构建的$H_A$和$b_A$的线性化点却可以改变，为了保证H矩阵的一致性，残差构建的$H_A$也使用$x_M$进行线性化，不会改变系统的能观性，但是这样做势必会引入线性误差。也就是说，残差$r_k$值的计算，使用$x_A$线性化点计算，$\frac{\partial r_k}{\partial x}$使用$x_M$线性化点处计算，这样可以构建一个新的$H_A$和$b_A$。除此之外，为了避免$b_M$描述的能量梯度不准确的问题，FEJ使用一阶泰勒展开对$b_M$进行修正，FEJ的公式描述如下：

$$ E_A(x) = E(x_A) + b_A(r_k(x_A), \frac{\partial r_k}{\partial x}|_{x=x_M})(x-x_A) + (x-x_A)^TH_A(x_M)(x-x_A) \\ E_M(x) = E(x_M) + b_M(x_M + x_A - x_M)(x-x_A) + (x-x_A)^TH_M(x_M)(x-x_A)\\ \frac{\partial b_M}{\partial x}|_{x=x_M}=H_M(x_M) \\ b_M(x_M + x_A - x_M) = b_M(x_M) + H_M(x_M)(x_A - x_M) \\ $$

其中：

$x_A$为某次优化中，残差线性化点；
$x_M$为marg的线性化点；
$E_A(x)$为残差对应能量值；
$E_M(x)$为marg对应的能量值；

从FEJ的公式描述可以发现，为了保证H矩阵的一致性，$H_A(x_M)$部分引入了线性化误差，在$b_A$计算过程中，$\frac{\partial r_k}{\partial x}|_{x=x_M}$部分引入了线性化误差，而$b_M(x_M+x_A - x_M)$部分使用泰勒展开进行了修正。

FEJ 非用不可？

通过上面公式的分析，可以发现，使用FEJ会不可避免的引入线性化误差（对残差部分来讲），而不引入FEJ又会导致系统的不一致性问题。貌似使用FEJ或者不使用FEJ都做不到完美。我认为FEJ并不是非使用不可，比如VINS中就没有使用FEJ，当然如果不使用FEJ的话，还是建议使用FEJ的$b_M$更新策略来维护$b_M$。甚至可以部分使用FEJ，DSO也是部分使用FEJ，来规避引入大的线性误差的风险。在DSO中，激活点的逆深度状态完全没有使用FEJ，这可能是因为激活点在经过一轮的滑动窗口优化后，可能不太稳定，如果固定逆深度的话，可能会引入较大的线性化误差。除此之外，DSO对$\frac{\partial r_k}{\partial \xi_{ji}}$、$\frac{\partial r_k}{\partial d_{pi}}$和$\frac{\partial r_k}{\partial C}$分阶段求解，$\frac{\partial r_k}{\partial \xi_{ji}}=\frac{\partial r_k}{\partial p_{j}}|_{x=x_A} \times \frac{\partial p_j}{\partial \xi_{ji}}|_{x=x_M} \quad \frac{\partial r_k}{\partial d_{pi}} = \frac{\partial r_k}{\partial p_j}|_{x=x_A} \times \frac{\partial p_j}{\partial d_{pi}}|_{x=x_M} \quad \frac{\partial r_k}{\partial C} = \frac{\partial r_k}{\partial p_j}|_{x=x_A} \times \frac{\partial p_j}{\partial C}|_{x=x_M}$，可能考虑到图像为非线性比较强的函数，因此对所有残差雅可比涉及图像梯度的部分都没有使用FEJ。

DSO在滑动窗口优化中的残差线性化阶段计算$\frac{\partial p_j}{\partial \delta \xi_{ji}}$、$\frac{\partial p_j}{\partial C}$和$\frac{\partial p_j}{\partial d_{pi}}$时使用了中心点的计算值代替整个pattern中每一个点的计算值，相当于减少了部分计算量，不过不清楚这么做是否会加重FEJ引入的线性化误差。

使用FEJ解决了系统不一致性问题后，就需要考虑先验的影响。DSO的系统求解中，主要有以下几种状态存在先验信息：

初始化完成后，加入到滑动窗口中的两个关键帧状态有先验。
初始化完成后，加入到滑动窗口中的激活点逆深度状态有先验。
由算法计算出的虚拟内参，有先验。

在给定某个状态的先验信息矩阵$H_P$后，先验信息构建的正规方程可以由下面的公式进行描述：

$$ E_P=\frac{1}{2}(x_A+\Delta x-x_P)^TH_P(x_P)(x_A+\Delta x-x_P)\\ b_P(x_P)=H_P(x_P)(x_A+\Delta x-x_P) $$

$E_P$为先验信息所对应的能量值；
$H_P$和$b_P$为先验信息构建的正规方程矩阵；
$x_P$为先验状态；

综上所述，当残差构建完成后，系统会根据提供的先验信息矩阵和最新边缘化得到的边缘化信息构建本次滑动窗口优化的正规方程，并进行迭代求解，构建的正规方程可以由下面的公式进行描述：

$$ H = H_A(x_M) + H_P(x_P) + H_M(x_M)\\ b = b_A(r_k(x_A), \frac{\partial r_k}{\partial x}|_{x=x_M}) + b_P(x_P) + b_M(x_M + x_A - x_M)\\ H \Delta x = -b $$

FEJ减少的计算量

在上面对FEJ的探讨中，我们知道了DSO中使用了部分FEJ的方案来解决系统的不一致性问题，又避免了引入大的线性化误差。使用这种方案竟还意外的减少了部分计算量，在4.1节中我们知道DSO需要将绝对量变换为相对量，需要求解$\frac{\partial {\xi_{ji}}}{\partial \xi_j}$、$\frac{\partial {\xi_{ji}}}{\partial \xi_i}$、$\frac{\partial {a_{ji}}}{\partial a_j}$、$\frac{\partial {a_{ji}}}{\partial a_i}$、$\frac{\partial {b_{ji}}}{\partial b_i}$和$\frac{\partial {b_{ji}}}{\partial b_j}$。而DSO的部分FEJ策略又将$\frac{\partial p_j}{\partial \xi_{ji}}$、$\frac{\partial r_k}{\partial \a_{ji}}$、$\frac{\partial r_k}{\partial \b_{ji}}$限制在线性化$x_M$处，因此相对量到绝对量转换的中间量的求解只需要在线性化点$x_M$处求解一次即可，在一定程度上可以减少一些计算量。

4.3 在解正规方程时，如何防止解在零空间中漂移？

对于某个等式$H \Delta x = -b$来讲，如果矩阵$H$不是满秩阵，那么必定存在$H x_{ns} = 0, x \ne \overrightarrow{0}$。其中$x_{ns}$为由$H$矩阵在零空间上的基组成的向量。这个$x_{ns}$也被称为解在零空间上的漂移。因为$H x_{ns} = 0, x \ne \overrightarrow{0}$总是成立的，因此不论$x_{ns}$漂移多少，$H (\Delta x + x_{ns}) = -b$总是成立的。也就是说在解正规方程时，如果不对零空间的漂移加以限制，那么解与不含漂移的解之间的误差就会很大。然而对于单目的VO系统来讲，系统总是有7个自由度，也就是说，H矩阵一定非满秩，并且与其行数差7，需要进行一些处理手段来保证正规方程得到的解不漂移。

DSO的源码里面定义了两种防止零空间漂移的方法，一种是基于SVD分解截断小奇异值求矩阵伪逆的方案，另一种是基于位姿矩阵伴随的性质求解世界坐标系零空间到局部坐标系零空间映射，并使用正交基投影的方式去掉零空间漂移的影响。

首先，我们先看下DSO求伪逆是如何防止零空间漂移的，假设目前完成了某次线性化，得到正规方程$H \Delta x = -b$，那么$H$的伪逆可以由下面的公式表示：

$$ H = U \Sigma V^T\\ H^{-1} = V \Sigma^{+}U^T\\ \Delta x^+ = H^{-1}b $$

其中：

$U$和$V$为酉矩阵（代表等距变换，列正交）；
$\Sigma$矩阵为对角矩阵，其对角上的值为奇异值；
奇异值为0的对应的 $V$矩阵的列为矩阵$H$的零空间的基，并且是正交基；
对$\Sigma$矩阵中的小奇异值置零后，将其非0奇异值取倒数后，转置得到$\Sigma^{+}$；
$H^{-1}$为$H$的伪逆；
$\Delta x^+$为去掉零空间漂移的正规方程的解；

通过对$\Sigma^+$矩阵和$V$矩阵的描述可知，$V$矩阵中0奇异值对应的列向量为零空间的一组正交基，然而$\Sigma^+$矩阵将小奇异值置零，在伪逆计算中，$\Sigma ^+$作用到了矩阵$V$的右侧，因此$V$矩阵0奇异值对应的列向量被$\Sigma ^+$矩阵作用后置零，因此得到的结果消除了零空间的影响。在DSO的源码里面有两种截断方式，一种是强制的7自由度截断，还有一种是定阈值截断法（小于这个阈值的奇异值置零）。

还有一种方式是通过世界坐标系零空间到相机坐标系零空间基转换的方式，直接求解出来相机坐标系对应的零空间的基，然后通过正交投影的方式得到零空间分量，最后减去即可。我们知道VO系统有7个自由度，即如果在世界坐标系上添加扰动，那么VO系统的约束仍然成立，因此世界坐标系上的零空间的基是恒定的，而相机坐标系上的零空间的基需要世界坐标系进行转换，下面的公式描述了这种转换关系：

$$ Exp(\delta \xi_c) T_{cw} = (Exp(\delta \xi_w) T_{wc})^{-1} \to Exp(\delta \xi_c) = T_{cw} Exp(-\delta \xi_w) T_{cw}^{-1} \to \delta \xi_c = -Ad_{T_{cw}} \times \delta \xi_w \\ $$

在DSO中使用世界坐标系零空间基上的正负两个扰动来推导出DSO相机坐标系对应的零空间基上的扰动，这里以$x$轴旋转$\phi_x$和比例因子$s$为例进行推导：

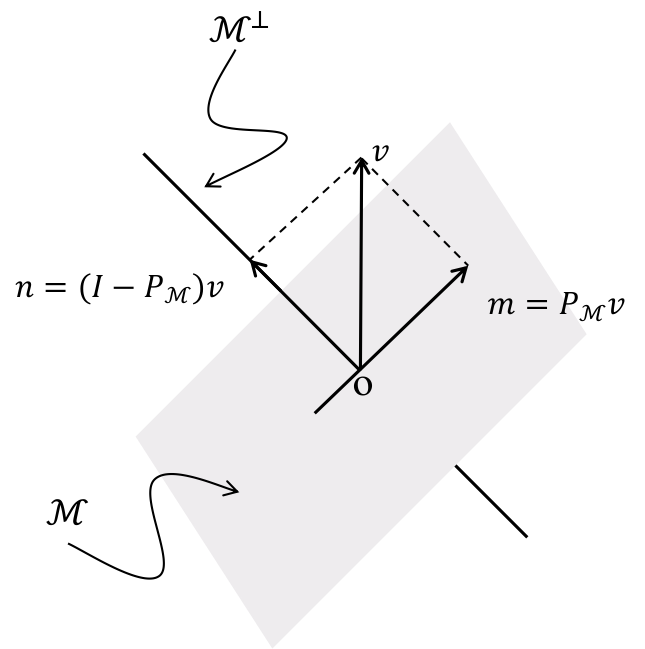
$$ \delta {\xi_{w}^{\phi_x}}_p = \begin{bmatrix} 10^{-3} & 0 & 0 & 0 & 0 & 0 \end{bmatrix}\\ \delta {\xi_{w}^{\phi_x}}_n = \begin{bmatrix} 10^{-3} & 0 & 0 & 0 & 0 & 0 \end{bmatrix}\\ \delta \xi_c^{\phi_x} = -\frac{1}{2\times 10^{-3}}Ad_{T_{cw}} \times (\delta {\xi_{w}^{\phi_x}}_p - \delta {\xi_{w}^{\phi_x}}_n)\\ \delta {s_w}_p = 1.0001\\ \delta {s_w}_p = \frac{1}{1.0001}\\ \delta \xi_c^s = \frac{1}{2\times 10^{-4}}Log(\begin{bmatrix} R_{cw} & \delta {s_w}_p t_{cw}\\ 0 & 1 \end{bmatrix} T_{cw}^{-1}) - Log(\begin{bmatrix} R_{cw} & \delta {s_w}_n t_{cw}\\ 0 & 1 \end{bmatrix} T_{cw}^{-1}) $$

在得到世界坐标系下的零空间基到相机坐标系下的零空间基转换后，通过正交投影的方式可以求得解在零空间中的分量，然后减去这个分量即可，下图是正交投影的例子，在 [2] 中推导得出$P_{\mathcal{M}}=M(M^TM)^{-1}M^T$，其中$M$为零空间中的基组成的矩阵，$P_{\mathcal{M}}v$代表的是$v$在零空间中的分量。

4.4 如何保证H矩阵非病态？

文章 [3] 中描述了病态矩阵出现的原因，针对正规方程$H\delta x=-b$这个公式，病态的$H$矩阵由于列相关性较高导致条件数过大，从而使得解$\delta x$收$b$矩阵的扰动较大。出现病态矩阵的根本原因是$H$矩阵中存在相关性较高的列，SVD分解后表现在$\Sigma$矩阵中存在极小的特征值，这与正规方程的解在零空间漂移存在一些关系，解在零空间漂移出现的原因是系统存在一定的自由度，即可以明确存在一些完全相关的列，而病态矩阵的出现是因为系统存在一些高度相关的列（不完全相关），从而在求解$\delta_x -H^{-1}b$时，小奇异值作用到$H^{-1}$上后，会产生较大的scale作用，从而难以应对$b$矩阵扰动情况。

普通病态矩阵可以通过截断SVD的方案来解决，即使用SVD对矩阵$H$进行分解，然后求$H$矩阵的逆时，可以将$\Sigma$矩阵中的小奇异值置零，将奇异值部分完全看做矩阵的零空间零空间来处理。DSO中的某个solver也使用了截断SVD的方式处理零空间问题，即给定某个阈值，小于这个阈值的奇异值都置零，这样可以同时解决零空间问题和病态矩阵问题。

DSO另外使用了一种对角线预处理的方式，来解决病态矩阵问题，对$H$和$b$矩阵进行预处理，旨在降低$H$矩阵的条件数。对角预处理的公式描述如下：

$$ W = \sqrt{diag(H) + 10 \times I}\\ H'=WHW\\ b'=Wb\\ x = -WH'^{-1}b'\\ $$

其中，$diag(H)$代表取H的对角线组成新的对角矩阵，使用这种对角预处理的手段确实可以减少矩阵H的条件数，但是比较有限。

5. 滑动窗口中的帧和点超出限定范围怎么办？

当滑动窗口的优化完成后，就到了边缘化判断和实施边缘化操作的阶段，我们知道DSO后端使用的是滑动窗口优化策略，因此为了保证优化的实时性，需要控制后端滑动窗口的规模，在DSO的源码中规定了理想的后端优化的规模，即5~7个关键帧和2000个左右的激活点。也就是说，当后端窗口中的关键帧或者激活点超出这个范围时，DSO就会使用边缘化的策略来控制滑动窗口的规模，以下是DSO的点管理和帧管理策略：

帧管理策略：

从优化提供的作用角度考虑，当某一帧$\frac{n_{i} + n_{p}}{n_{m} + n_{d} + n_i + n_p} < 0.05$则判断当前帧需要被边缘化，其中$n_{i}$代表未成熟点的个数，$n_{p}$代表该帧中激活点的数目，$n_m$代表该帧被边缘化点的数目，$n_d$代表该帧被丢掉点的数目，如果可以对优化起作用的点数目（$n_i + n_p$）占所有点的比例小于5%时，则判断该帧对优化提供的作用较少，标记为边缘化；
从曝光参数上考虑，计算某一帧和最新帧之间的光度参数$a_{ji}>=0.7$（这里的$a_{ji}$和初始化中的$a_{ji}$意义相同），则认为该帧和最新帧之间的亮度变化太大（环境光变化大），则标记当前帧为边缘化；
在时间轴上考虑，保证距离最新帧newFH较近的3帧不被边缘化；
在距离轴上考虑，提出启发式距离评价方法，距离评分公式为$s(I_i)=-\sqrt{d(i, 1)}\times \sum_{j\in[3,n],j\ne i}{d(i,j)^{-1}}$，将评分最小的帧标记为边缘化帧；
值得注意的是，每次只边缘化一帧，上面的条件从上到下依次判断，如果满足某一个条件则标记边缘化帧后退出。

点管理策略：

逆深度小于0或者没有参与优化的点，被丢掉drop
判断某个点对后续滑动优化的作用：
- 某一帧被边缘化后，点残差保留太少，则认定对后续滑窗优化作用不大
- 最新帧看不到该点，则认定为对后续滑窗优化作用不大
- 针对那些残差比较少的点，是新加入的点，认定对后续滑窗优化的作用较大（源码里面还做了单独的判断，这个判断是否不需要做，仅对作用不大的条件进行判断不就好了？）
- 在最近两次滑窗优化中都被判断为是outlier的点，则认定对后续滑窗优化作用不大
判断某个点是否是内点：
- 要求残差数量要大于某个阈值
- 要求被判断为是inlier的残差数量要大于某个阈值
如果判断某个点对后续滑窗优化的作用不大或者某个激活点的host帧为待被边缘化的帧
- 如果这个点被判断为内点
  - 判断该点的$H_{dd} > 50$，$H_{dd}$是该点在滑窗优化中计算的Hessian，如果不满足则标记为丢掉；
  - 否则标记为边缘化掉；
- 如果这个点被判断为外点，则标记为丢掉。

假设下图中，点$p_1$需要被丢掉，点$p_2$、$p_3$、帧$kf_1$需要被边缘化掉。

具体执行边缘化的流程可以由下图进行描述，首先根据要被边缘化的残差构建Hessian和b，值得注意的是，线性化点为$x_M$，在实施边缘化操作之前，还需要考虑点的先验信息，需要加上确定被边缘化的状态的先验Hessian和先验b，然后先边缘化点，最后边缘化帧。使用schur分解的方式实现，下面的图描述了这一过程：

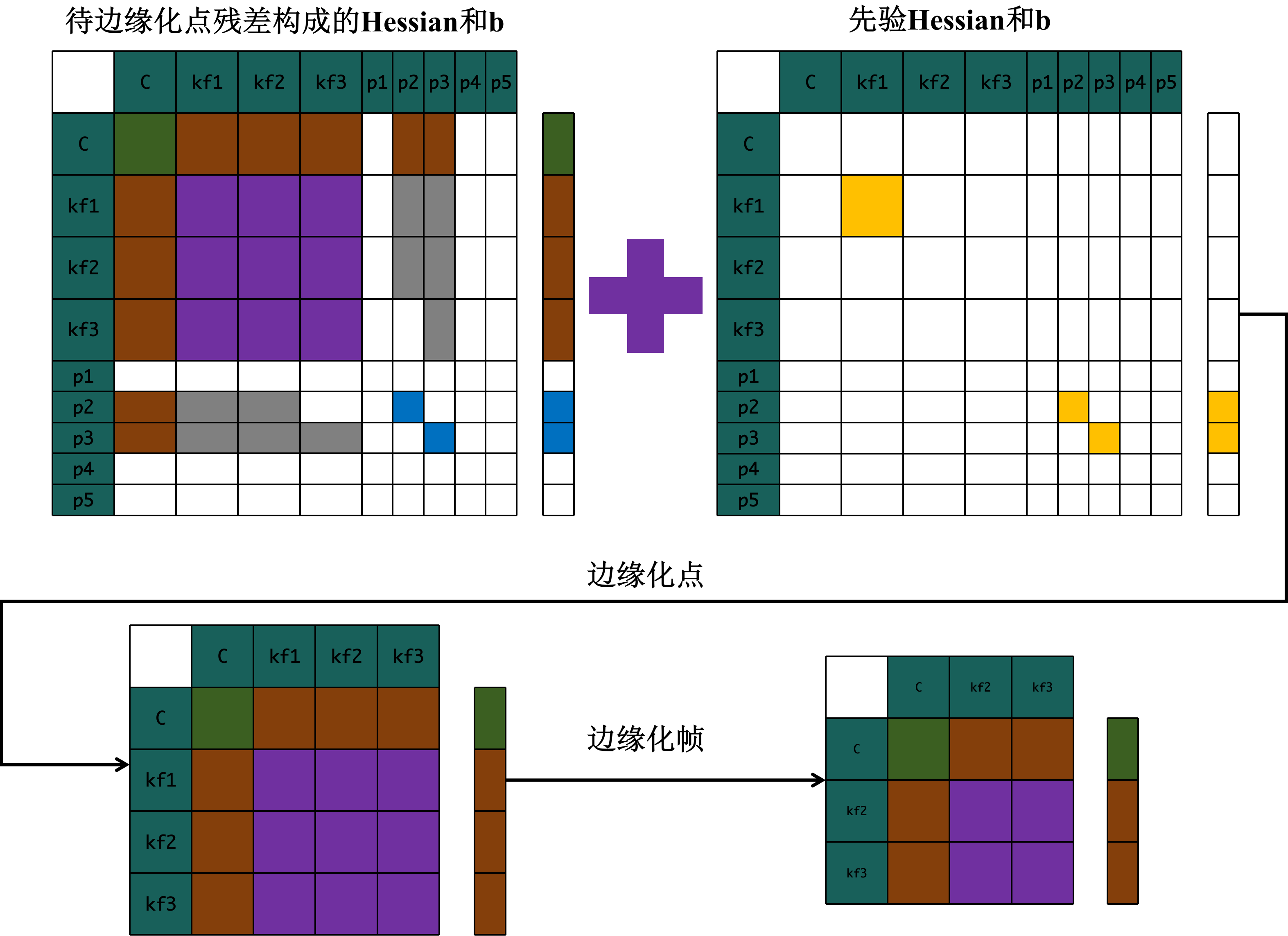
为什么先边缘化点再边缘化帧？

在点管理策略中可以发现，某个帧如果被判断为要被边缘化掉的话，该帧上的所有激活点都要被丢掉或者边缘化掉。并且实施边缘化时需要先边缘化掉点，然后边缘化掉帧。这么做的原因在于，防止边缘化帧时导致点与点之间的Hessian变稠密。如果点与点之间的Hessian不在稀疏，那么整个优化过程将变的极其复杂，schur分解加速优化将不再成立，求解正规方程将非常缓慢。

Reference

[1] T. -C. Dong-Si and A. I. Mourikis, “Consistency analysis for sliding-window visual odometry,” 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 2012, pp. 5202-5209, doi: 10.1109/ICRA.2012.6225246.

[2] Meyer C D. Matrix analysis and applied linear algebra[M]. Society for Industrial and Applied Mathematics, 2023.

[3] 机器学习中的矩阵方法(附录A)：病态矩阵与条件数

孙善路-github 对SLAM和DL感兴趣的理工男

孙善路-bilibili 对SLAM和DL感兴趣的理工男

有什么问题吗，有任何问题欢迎你在下面评论留言或者邮件联系我！

Comments