DSO中的优化模型

在之前的DSO中的去畸变操作文章中，讲到DSO考虑了相机的成像过程对图像像素的影响：

在有光度参数的条件下，DSO使用$G^{-1}(I)$非线性响应函数的逆过程和渐晕函数$V(x)$进行图像的光度去畸变操作，可以得到由能量单位组成的去光度畸变的图像。
在没有光度参数的条件下，DSO使用仿射参数a和b来模拟光度参数的去畸变过程。
在DSO中的去畸变操作文章中，也进行了讨论，即去畸变得到的像素能量并不能保证同一点的一致性，因为还没有考虑曝光时间的影响。

1. 构建优化模型

SLAM十四讲中提到，直接法会直接使用像素的灰度值，构建优化模型的残差，其公式表示为$r_k=I_i(p_i)-I_j(p_j)$。由于DSO引入了仿射参数去光度畸变的操作，同时考虑了曝光时间对其一致性的影响，构建的残差应该为：

$$ r_k = \frac{1}{t_i}(e^{a_i} I_i(p_i) - b_i) - \frac{1}{t_j}(e^{a_j} I_i(p_i) - b_j) $$

通过一些移项和变换的操作，并考虑像素块pattern的影响，就可以得到DSO论文里面给出的残差模型了：

$$ E_{p_j} = \sum_{p \in \mathcal{N_{p_i}}}{\left | \left | (I_j(p') - b_j) - \frac{t_je^{a_j}}{t_ie^{a_i}}(I_i(p) - b_i) \right | \right | }_\gamma \\ P_{norm} = \pi^{-1}(p) \\ P' = R_{ji} P_{norm} + t_{ji} d_{pi} \\ P_{norm}' = \frac{P'}{P'_Z} \\ p' = \pi(P'_{norm}) $$

其中：

$t_i$和$t_j$分别为$i$帧和$j$帧的曝光时间，如果不存在曝光时间，则设定$t_i=t_j=1$；
$a_i$和$b_i$为$i$帧的仿射参数，$a_j$和$b_j$为$j$帧的仿射参数，如果存在光度参数和曝光时间，则设定$a_j = a_i = b_j = b_i = 0$；
$I_i$和$I_j$分别为$i$帧和$j$帧的去畸变图像，设定$i$帧为参考帧，而$j$帧为待估计帧；
$p$和$p'$分别为$i$帧上的像素点和$j$帧上的像素点，其中$p'$是$p$经过反向投影，位姿变换和正向投影得到的像素点；
$\pi$函数指的是从归一化坐标系到像素坐标系的投影，$\pi^{-1}$是$\pi$的反函数；
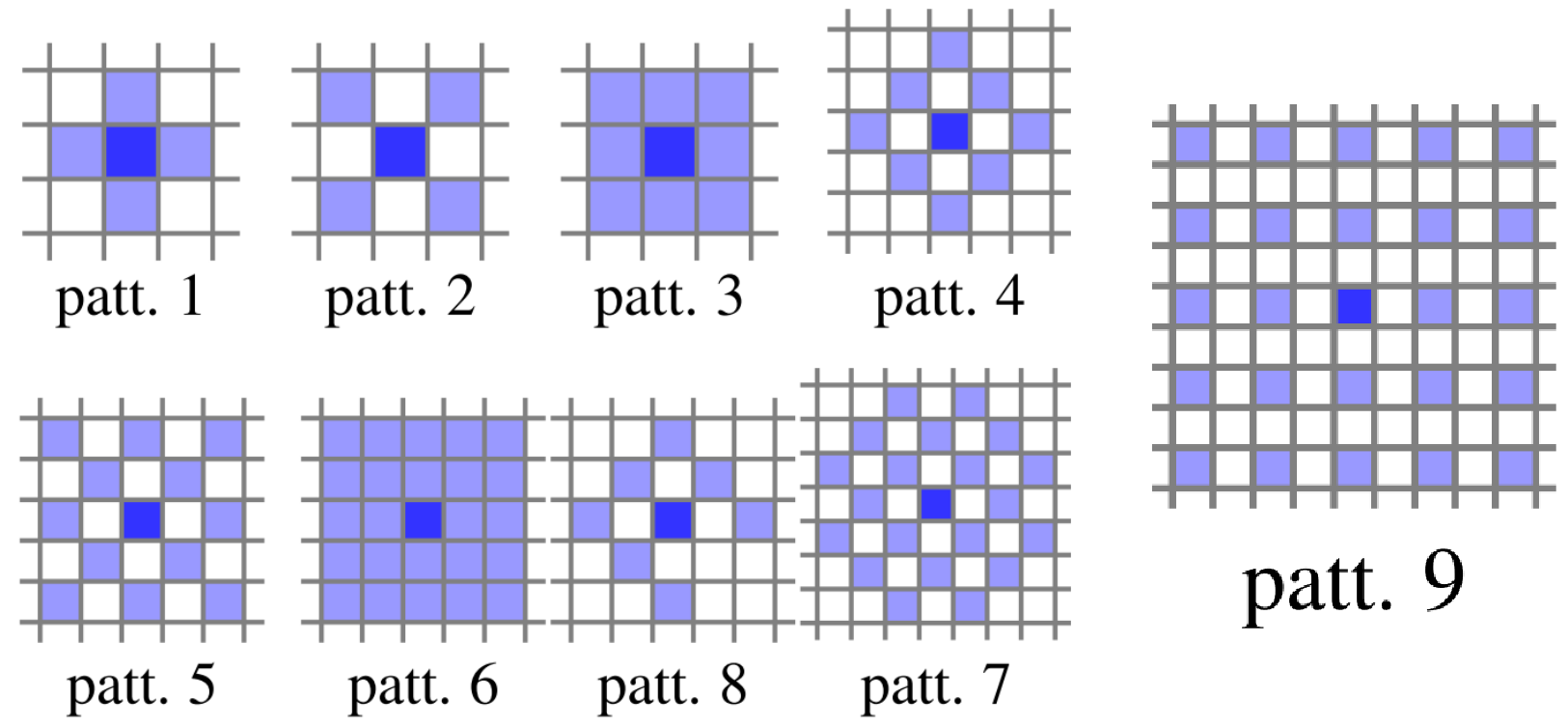
$\mathcal{N_{p_i}}$为以$i$帧上的像素点$p_i$为中心的像素块，在DSO的论文中，把他叫做一个pattern，DSO引入pattern的概念，认为在一个pattern上，所有像素的逆深度$d_{pi}$值保持一致，下图中是在DSO论文中讨论的一些pattern；

DSO的投影过程与普通BA之间存在区别？

在DSO构建的模型中，有一个与普通BA过程存在明显不同的地方，即在构建完成反向投影后，并不会使用$R_{ji}\frac{P_{norm}}{d_{pi}}+t_{ji}$来求解真实的3d点，而是使用$R_{ji}P_{norm}+t_{ji}d_{pi}$的方式，乘在了右边，构建了一个虚拟的3d点，这个虚拟3d点在坐标系原点真实3d的直线上，因此真实点和虚拟点之间对应着一个相同的归一化坐标系下的点。这么构建有一个比较明显的优势，即针对$d_{pi}$求导时，会变的比较简单。

2. 求解模型雅可比

现在，令$r_k=I_j(p')-\frac{t_je^{a_j}}{t_ie^{a_i}}I_i(p)+\frac{t_je^{a_j}}{t_ie^{a_i}}b_i-b_j$，考虑使用GN法或者LM法求解这个优化问题，因此需要求解残差$r_k$对待优化量的雅可比矩阵，后续无论是需要为优化模型添加核函数，或者是求解优化模型的海塞矩阵H，都可以通过残差对待优化量的雅可比矩阵进行变换得到。

2.1 残差对位姿的雅可比矩阵

根据链式求导法则，残差对位姿$T_{ji}$的左侧扰动$\xi$的雅可比矩阵$\frac{\partial{r_k}}{\partial{{\xi_{ji}}}}$：

$$ \frac{\partial{r_k}}{\partial{{\xi_{ji}}}} = \frac{\partial{r_k}}{\partial I_j} * \frac{\partial{I_j}}{\partial{p'}} * \frac{\partial{p'}}{\partial{P_{norm}'}} * \frac{\partial{P_{norm}'}}{\partial{P'}} * \frac{\partial{P'}}{\partial{\xi_{ji}}} $$

$\frac{\partial{r_k}}{\partial I_j}$，根据残差公式，可以看出来$\frac{\partial{r_k}}{\partial I_j}=1$；
$\frac{\partial{I_j}}{\partial{p'}}$，可以定义为$p'$在图像$I_j$上的像素梯度，以$[d_x,d_y]$进行表示；
$\frac{\partial{p'}}{\partial{P_{norm}'}}$，这部分表示的是归一化坐标系到像素坐标系的投影过程，其雅可比矩阵可以使用如下公式进行表示；

$$ \frac{\partial{p'}}{\partial{P_{norm}'}} = \begin{bmatrix}f_x&0\\0&f_y\end{bmatrix} $$

$\frac{\partial{P_{norm}'}}{\partial{P'}}$，这部分表示的是虚拟点$P'$到归一化坐标系的投影过程，根据公式不难推导出,其雅可比矩阵可以由下面的公式进行表示：
$$ \frac{\partial{P_{norm}'}}{\partial{P'}} = \begin{bmatrix}\frac{1}{P_Z'}&0&-\frac{P_X'}{P_Z'^2}\\0&\frac{1}{P_Z'}&-\frac{P_Y'}{P_Z'^2}\end{bmatrix} $$
$\frac{\partial{P'}}{\partial{\xi_{ji}}}$，这部分表示的是虚拟3d点位姿$T_{ji}$左乘扰动$\xi_{ji}$的雅可比矩阵，在视觉SLAM十四讲的中86页中推导过，这里只不过是针对虚拟点做了一些变换，可以得到$\frac{\partial{P'}}{\partial{\xi_{ji}}}=[d_{pi}I,-P'^{\wedge}]$

综上，通过链式法则将5部分的雅可比矩阵相乘可得残差对$T_{ji}$的左乘雅可比矩阵为:

$$ \begin{align*} \frac{\partial{r_k}}{\partial{\xi_{ji}}}&= \frac{1}{P_Z'} \begin{bmatrix} d_x&d_y \end{bmatrix} \begin{bmatrix} f_x & 0 \\ 0 & f_y \end{bmatrix} \begin{bmatrix} 1 & 0 & -\frac{P_X'}{P_Z'} \\ 0 & 1 & -\frac{P_Y'}{P_Z'} \\ \end{bmatrix} \begin{bmatrix} d_{pi}&-P'^{\wedge} \end{bmatrix}\\ &= \begin{bmatrix} d_xf_x&d_yf_y\end{bmatrix} \begin{bmatrix} \frac{d_{pi}}{P_{Z}'} & 0 & -\frac{d_{pi}}{P_{Z}'}\frac{P_{X}'}{P_{Z}'} & -\frac{P_{X}'P_{Y}'}{P_{Z}'^2} & 1+\frac{P_{X}^{2}}{P_{Z}^{2}} & -\frac{P_{Y}'}{P_{Z}'} \\ 0 & \frac{d_{pi}}{P_{Z}'} & -\frac{d_{pi}}{P_{Z}'}\frac{P_{Y}'}{P_{Z}'} & -1-\frac{P_{Y}^{2}}{P_{Z}^{2}} & \frac{P_{X}'P_{Y}'}{P_{Z}^{2}} & \frac{P_{X}'}{P_{Z}'} \end{bmatrix} \end{align*} $$

2.2 残差对$p_i$点逆深度的雅可比矩阵

根据链式求导法则，残差对点的逆深度$d_{pi}$的雅可比矩阵$\frac{\partial{r_k}}{\partial{{d_{pi}}}}$：

$$ \frac{\partial{r_k}}{\partial{{d_{pi}}}} = \frac{\partial{r_k}}{\partial I_j} * \frac{\partial{I_j}}{\partial{p'}} * \frac{\partial{p'}}{\partial{P_{norm}'}} * \frac{\partial{P_{norm}'}}{\partial{P'}} * \frac{\partial{P'}}{\partial{d_{pi}}} $$

可以发现，残差对$p_i$点逆深度的链式求导的雅可比矩阵的前4部分都是相同的，因此只需要考虑$\frac{\partial{P'}}{\partial{d_{pi}}}$这部分的雅可比即可，从公式中不难推导出：

$$ \frac{\partial{P'}}{\partial{d_{pi}}}=t_{ji} $$

综上，通过链式法则将5部分的雅可比矩阵相乘可得残差对$d_{pi}$的雅可比矩阵为:

$$ \begin{align*} \frac{\partial{r_k}}{\partial{d_{pi}}}&= \frac{1}{P_Z'} \begin{bmatrix} d_x&d_y \end{bmatrix} \begin{bmatrix} f_x & 0 \\ 0 & f_y \end{bmatrix} \begin{bmatrix} 1 & 0 & -\frac{P_X'}{P_Z'} \\ 0 & 1 & -\frac{P_Y'}{P_Z'} \\ \end{bmatrix} \begin{bmatrix} t_{ji}^X\\t_{ji}^Y\\t_{ji}^Z \end{bmatrix}\\ &= \frac{1}{P_Z'}[d_xf_x(t_X^{ji}-\frac{P_X'}{P_Z'}t^Z_{ji})+d_yf_y(t_Y^{ji}-\frac{P_Y'}{P_Z'}t^Z_{ji})] \end{align*} $$

2.3 残差对光度仿射参数的雅可比矩阵

DSO在不同的阶段对光度仿射参数做了不同程度的处理，其主要表现在初始化阶段、前端跟踪阶段和后端滑窗阶段。其中，初始化阶段和前端跟踪阶段主要注重相对仿射参数$a_{ji}$和$b_{ji}$，而在后端滑窗优化阶段中则更加注重全局的仿射参数$a_j$、$b_j$、$a_i$和$b_i$。

我打算分别在初始化、前端跟踪和后端滑窗优化三篇文章中单独对”DSO对仿射参数处理”进行解析说明，在这篇文章中就不过多赘述了。

3. 模型在后端优化中的问题

正如我在2.3小节中所描述的，DSO的模型在后端优化中会产生一些问题，原因在于后端优化的参数量为全局量，而不是相对量。即是global而非local。

其中在后端中需要特殊处理的参数主要有相对位姿$T_{ji}$转变为绝对位姿$T_{jw}$和$T_{iw}$、相对光度仿射参数$a_{ji}$和$b_{ji}$转变为全局光度仿射参数$a_j$，$b_j$，$a_i$和$b_i$。

模型如何在后端优化中解决这个问题的说明，我会在DSO滑窗优化后端中单独进行说明。

提前透漏

可以提前说明的是，在相对位姿转绝对位姿部分，DSO使用的是位姿矩阵伴随的性质，而光度仿射参数的转换则采用的是雅可比矩阵中转变换的方法。

孙善路-github 对SLAM和DL感兴趣的理工男

孙善路-bilibili 对SLAM和DL感兴趣的理工男

有什么问题吗，有任何问题欢迎你在下面评论留言或者邮件联系我！

Comments

DSO中的优化模型

1. 构建优化模型

2. 求解模型雅可比

2.1 残差对位姿的雅可比矩阵

2.2 残差对\(p_i\)点逆深度的雅可比矩阵

2.3 残差对光度仿射参数的雅可比矩阵

3. 模型在后端优化中的问题

Comments

Keep Reading

Published

Category

Tags

Contact Me