DSO中的去畸变操作

1. 像素去畸变

1.1 畸变模型

DSO中引入了不同的畸变模型，来解决不同相机的像素畸变问题，除了我们在SLAM十四讲里面熟知的RadTan畸变模型外，还有FOV和KannalaBrandt畸变模型。不同的像素畸变模型的公式由下面的公式给出：

首先是我们熟知的RadTan径向切向畸变模型，可以根据畸变程度选择不同参数数量进行配置计算，常用的有三参数法（\(k_1\),\(p_1\),\(p_2\)）和五参数法（\(k_1\),\(k_2\),\(k_3\),\(p_1\),\(p_2\)）：

然后是FOV视野畸变模型，仅有一个参数\(\omega\)：

最后是KannalaBrandt光度畸变模型，有四个参数\(k_1\),\(k_2\),\(k_3\),\(k_4\)：

1.2 DSO中畸变模型转Pinhole逻辑

当然，这里的畸变模型并不是我想向大家进行解析的重点，DSO将这种像素畸变模型向小孔成像模型Pinhole进行了转换，而这个转换的逻辑，是我想给大家分享的重点！这里三种不同的畸变模型，我以\(d(p,K)\)来进行表示，这里的\(p\)表示归一化坐标系下的某个实际点，而\(K\)表示畸变模型的参数。

1. 在归一化坐标系上，划定一块足够大的区域\(S\)，在DSO的源码里面是\(x\in[-5,+5],y\in[-5,+5]\)，试图通过在\(x=0\)和\(y=0\)的区域线段上，找到一组极限位置\(X_{min}\)、\(X_{max}\)、\(Y_{min}\)和\(Y_{max}\)，作为初始的粗略归一化区域（这个区域包含足够多的像素信息）。
2. 在X=0轴方向上，以y划分为10万个刻度点，使用这些点向畸变坐标系进行投影，试图找到一个\(Y_{min}\)和\(Y_{max}\)，对应的这两个点的像素投影点都应在畸变像素坐标系内。
3. 在Y=0轴方向上，使用上面一样的策略，寻找\(X_{min}\)和\(X_{max}\)。
4. 在获得的极限位置轴上，取点（点的个数可以是畸变图像的宽度或者高度，以保证足够的分辨率），进行畸变和投影获得畸变像素坐标，判断像素坐标是否在图像范围内。
5. 如果所有点都在像素图像范围内，则认为这个这个轴的位置是合理的。
6. 如果存在点不在像素图像范围内，则需要将这个轴的位置进行向内移动，源码中是*0.995，以此来达到向内移动的效果。
7. 注意，当X轴和Y轴部分都需要向内移动时，源码中为了防止额外的像素损失，仅尺寸较大的那一轴进行移动。
8. 总的来说，DSO在实现畸变模型到纯小孔成像模型之间转换的时候，使用了两步法实现，首先，通过X=0和Y=0两个轴上的点确定一个较粗粒度的归一化区域，因为使用的是归一化中心点，因此这个区域肯定可以覆盖绝大部分的可视像素信息。然后再不断的投影四个极限轴上的点来实现轴的缩放，因此来获取一个精确的归一化区域。

使用上述说明的方式，可以获得一个归一化区域，这个区域内的所有点向畸变像素坐标系投影的结果都会在畸变图像范围内。在给定目标图像的宽度w和高度h后，可以计算获得pinhole条件下的内参矩阵K:

最终可以得到：

在得到纯小孔成像模型的相机内参矩阵K后，为了更加方便的实现畸变图像到非畸变图像的转换，DSO维护了一组映射表remapX和remapY。这组映射表的构建逻辑也比较简单，可以通过下面的这张图进行表示：

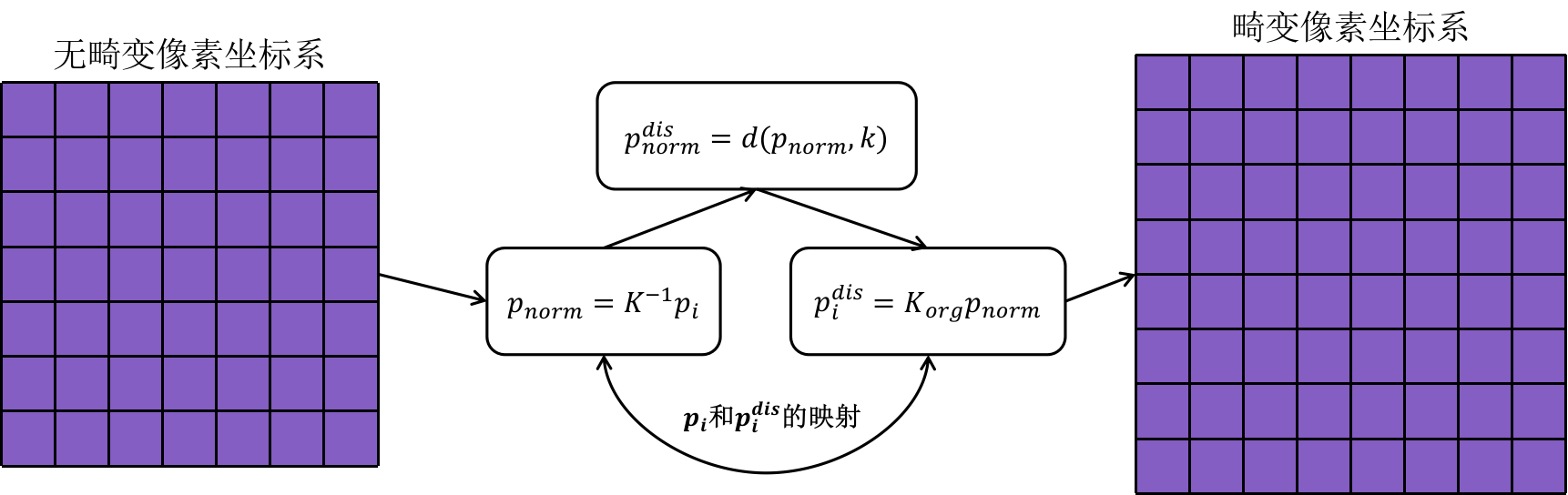
针对无畸变坐标系下的某个像素点\(p_i\)，通过反向投影到归一化坐标系下得到\(p_{norm}\)，然后使用畸变参数模型在归一化坐标系下对点\(p_{norm}\)进行畸变处理得到点\(p_{norm}^{dis}\)，然后使用原来的相机内参\(K_{org}\)进行投影，得到无畸变像素坐标系点\(p_i\)和有畸变像素坐标系\(p_i^{dis}\)之间的映射关系。DSO将这部分对应起来的映射关系存储到remapX和remapY中，以便快速的进行无畸变图像的构建。这里还需要注意的是，使用映射表得到畸变像素坐标后，需要使用双线性插值实现像素值或者说是像素能量值（光度去畸变后）的精确获取。

2. 光度去畸变

2.1 光度畸变模型

DSO的作者考虑了相机的成像过程，针对形成漫反射的某个点p来讲,它会产生辐射\(B_i(x)\)，相机的感光器件会接收到这个这个点的辐射\(B_i(x)\)。但是由于辐射在相机的透镜中会发生一些扭曲，造成相机成像的渐晕现象（中间部分接收的辐射较高，而周围的较低），这种渐晕会被建模称\(V(x)\)，一般会用一张和成像尺寸相同的灰度图来表示，下面是TUM/sequence_29数据集中的渐晕图表示。

相机的感光器件在一定的曝光时间\(t_i\)内（很短的一段时间内），对辐射进行积分，假设在曝光时间内的辐射恒定那么感光器件获取到的能量值可以通过\(IR_{acc}(x)=t_iV(x)B_i(x)\)进行表示。

除此之外，相机并不会直接将能量作为像素值的输出，而是会经过相机的非线性响应函数\(G\)进行转换，\(I_i(x)=G(t_iV(x)B_i(x))\)，而\(G^{-1}\)一般通过单调递增的256个数值进行表示，即索引部分为像素值，而值部分对应的是某个适应的能量值。

因为DSO这种直接法会直接跟像素值打交道，为了避免渐晕\(V(x)\)和曝光时间\(G\)响应函数的干扰，DSO在这里进行了光度矫正处理，矫正处理的结果为：

通过深度思考发现，如果光照恒定的条件下，不同点产生的辐射值\(B_i(x)\)是相同的，但是这里的光度矫正为什么还会存在曝光时间\(t_i\)的影响呢？

我认为，这种疑问考虑是完全正确的，这里的光度矫正确实没有去掉曝光时间\(t_i\)的影响，但是曝光时间这部分的影响是在优化的能量函数中进行考虑的。能量函数的建模部分我会单独进行讲解，这里只需要记住DSO会在能量函数建模中考虑曝光时间的影响即可。

2.2 无光度参数的解决方案

在2.1部分，光度畸变模型中，要求需要对相机的光度参数部分进行标定，这会涉及到渐晕\(V(x)\)的标定、非线性响应函数\(G(I)\)的标定，以及曝光时间的获取。

然而在实际的数据集中，这些参数绝大部分的数据集是没有的，因此DSO提供了一种无光度参数的解决方案，即使用仿射函数的方式实现模拟光度校正，并且认定曝光时间\(t_i\)为1，即：

DSO的论文里面还这样描述：这里乘法因子使用\(e^{a_i}\)而不是直接使用\(a_i\)的原因是，使用指数函数，既可以防止其乘法项变为负数，又可以避免因乘法漂移而产生的数值问题。

喜欢这篇文章吗？喜欢就分享吧: Twitter ❄ Facebook ❄ Email

孙善路-github 对SLAM和DL感兴趣的理工男

孙善路-bilibili 对SLAM和DL感兴趣的理工男