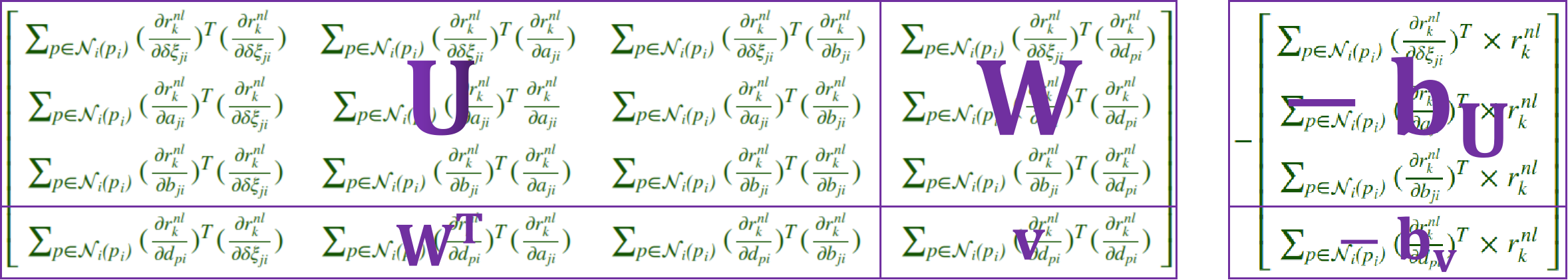在这篇文章中,我会对DSO初始化的过程和初始化中的一些要点进行讲解说明。作为一个单目视觉VO系统,DSO也采用了多帧初始化的策略,即首先在初始化参考帧上进行提点操作,然后根据不同的帧来优化初始化参考帧上点的逆深度估计,初始化的优化模型是在DSO中的优化模型文章中提到的优化模型基础上,考虑了逆深度的连续性和平移距离构建的,并且使用了Schur消元来加速初始化中的优化过程。
在DSO的初始化过程中还使用了图像金字塔(从粗到精的优化)来提高鲁棒性,并构建点的同层相邻点和上层父点之间的联系,实现点的逆深度传递。除此之外,DSO在初始化过程中还对相对光度仿射参数进行了处理,下面是我对这些要点的详细说明:
1. 初始化中对仿射参数的处理
我在DSO中的优化模型文章中提到了DSO的优化残差,可以使用下面的公式进行描述。
$$
r_k = (I_j(p') - b_j) - \frac{t_je^{a_j}}{t_ie^{a_i}}(I_i(p) - b_i)
$$
可以看到,公式中涉及到了参考帧\(i\)待求解帧\(j\)的绝对光度仿射参数,为了简化这部分对求导的影响,DSO构造了相对仿射参数来代替绝对仿射参数,即令\(e^{aji}=\frac{t_je^{a_j}}{t_ie^{a_i}}\),\(b_{ji}=b_j - a_{ji}b_i\)得公式(2):
$$
r_k = I_j(p')-e^{a_{ji}}I_i(p)-b_{ji}
$$
为什么不使用\(a_{ji}\)而是使用\(e^{a_{ji}}\)?
首先,如果使用\(a_{ji}\)来代替\(\frac{t_je^{a_j}}{t_ie^{a_i}}\)话,就会要求\(a_{ji}>0\)的,因此模型会从原来的无约束优化问题变成了部分变量的有约束优化问题,会增加整个优化过程中的难度。因此为了避免这个问题,DSO中使用了\(e^{a_{ji}}\)来代替\(\frac{t_je^{a_j}}{t_ie^{a_i}}\)而不是\(a_{ji}\)。
为了解决这个优化问题,除了DSO中的优化模型文章中求解的一些雅可比矩阵外,还需要求解残差对相对光度仿射参数的雅可比矩阵,从构建的残差公式中不难得到:
$$
\frac{\partial r_k}{\partial a_{ji}} = e^{a_{ji}}I_i(p)\\
\frac{\partial r_k}{\partial b_{ji}} = -1
$$
2. 初始化优化模型中的惩罚项
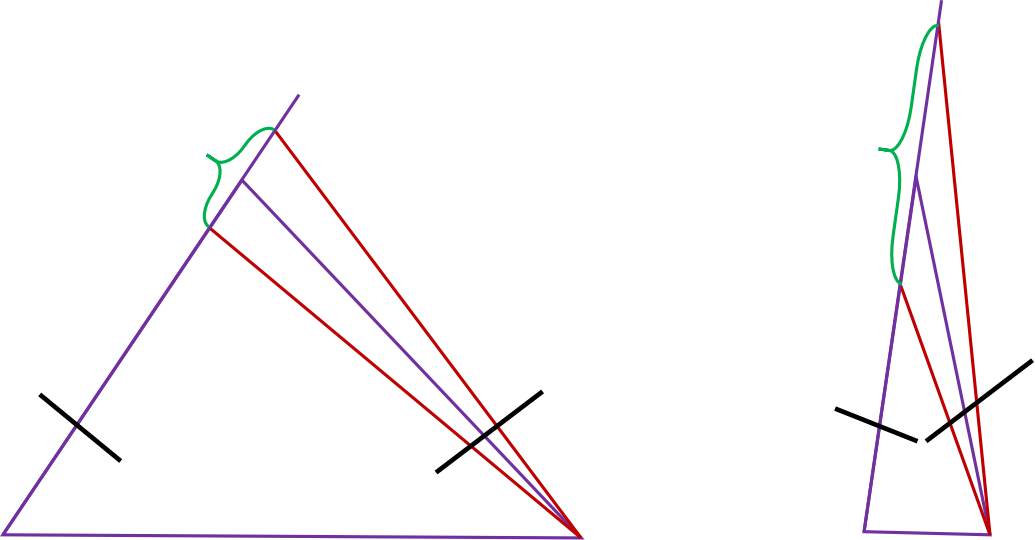
接下来,我们需要讨论的是,为什么DSO在初始化过程中需要一个相对大并且准确估计的相对平移距离\(t_{ji}\)。现在看下图的一个位姿估计过程,对比大平移距离\(t_{ji}\)和小平移距离\(t_{ji}\)的两张优化结果。可以发现,如果投影到\(j\)帧上的像素点存在1个像素的误差,大平移距离对应的点\(p_i\)的深度变化可以由图像左侧的绿色大括号表示,而小平移距离对应的点\(p_i\)的深度变化由右侧的绿色大括号表示。可以看出,小平移距离估计的点\(p_i\)的深度受投影像素误差影响比较大。因此DSO才会针对平移距离构建不同的优化目标函数,试图找到一个准确且足够大的\(t_{ji}\),来保证初始化参考帧上的点\(p_i\)逆深度的稳定性和准确性。
2.1 平移距离不足时的惩罚项
DSO在初始化过程中还考虑了平移距离和逆深度连续性的影响,DSO认为在初始化过程中,
输入的普通帧\(j\)和初始化参考帧\(i\)的平移距离应该达到某个阈值才认为\(j\)帧对参考帧上点逆深度起作用,为了确保在优化过程中得到的相对平移距离足够可靠,DSO在未达到足够的平移距离之前,会对平移距离添加惩罚项,除此之外还会对点的逆深度做一个尺度约束,因此在平移距离不够的条件下,DSO构造的优化目标函数如下:
$$
E_f=\sum_{p_i\in R_f}{\sum_{p\in \mathcal{N}_i(p_i)}{||I_j(p')-e^a_{ji}I_{R_f}(p)-b_{ji}||_{\gamma}}}+E_l\\
E_l=\frac{\alpha_W}{2} \sum_{p_i\in R_f}{((d_{pi}-1)^2+||t_{ji}||^2_2)}
$$
其中:
- \(E_f\)部分为平移量不足条件下的优化目标函数;
- \(E_l\)部分包含了逆深度尺度惩罚项\((d_{pi} - 1)^2\)和相对平距离的惩罚项\(||t_{ji}||^2_2\);
- \(\alpha_W\)代表调节正则化项部分的超参数,从而在一定程度上改变优化的侧重方向;
- \(R_f\)代表是初始化参考帧
针对\(E_l\)的惩罚项部分,\(E_l^{p_j}\)的整个组成部分相对简单,可以直接求解惩罚项的雅可比矩阵\(J_l\)和海塞矩阵\(H_l\),而不必使用高斯牛顿法利用残差项的雅可比变换得到:
$$
\frac{\partial E_l^{p_j}}{\partial x} = J_{p_i}=\begin{bmatrix}
t_{ji}^T & 0_{1 \times 3} & 0 & 0 & d_{pi}-1
\end{bmatrix}
\\
\frac{\partial^2 E_l^{p_j}}{\partial x^2} = H_{pi}=
\begin{bmatrix}
\begin{bmatrix}
I_{3\times 3} & \mathbf{0_{3\times3}}\\
\mathbf{0_{3\times3}} & \mathbf{0_{3\times3}}
\end{bmatrix} & \mathbf{0_{6 \times 1}} & \mathbf{0_{6 \times 1}} & \mathbf{0_{6 \times 1}}\\
\mathbf{0_{1 \times 6}} & 0 & 0 & 0 \\
\mathbf{0_{1 \times 6}} & 0 & 0 & 0 \\
\mathbf{0_{1 \times 6}} & 0 & 0 & 1 \\
\end{bmatrix}
$$
\(E_l^{p_j}\)和\(E_l\)的区别
值得注意的是,\(E_l^{p_j}\)的能量值,代表是初始化参考关键帧\(R_f\)上的点\(p_i\)向\(p_j\)部分投影这一约束贡献的系统能量值,或者说是贡献的优化目标函数值。惩罚项的海塞矩阵\(H_l\)可以由所有的\(H_l^{p_j}\)组合而成,即相同的约束部分可以加和,而不用的约束部分需要拓展组成一个大矩阵\(H_l\),当然,雅可比矩阵也是如此。
2.2 平移距离足够时的惩罚项
当平移距离足够时,DSO认为初始化参考帧\(i\)中的像素点\(p_i\)的逆深度会有一个相对稳定、准确且尺度一致(因为使用了\((d_{pi}-1)^2\)作为尺度惩罚项)的值,这时,DSO会去掉对平移距离的惩罚项,同时对逆深度进行期望约束,这里的期望值\(iR\)考虑了当前点\(p_i\)和周围点的逆深度关系,即逆深度的平滑性,得到的优化目标函数如下:
$$
E_f=\sum_{p_i\in R_f}{\sum_{p\in \mathcal{N}_i(p_i)}{||I_j(p')-e^a_{ji}I_{R_f}(p)-b_{ji}||_{\gamma}}}+E_l\\
E_l=\frac{\alpha}{2} \sum_{p_i\in R_f}{(d_{pi}-iR_{i})^2}
$$
其中:
- \(E_f\)部分为平移量足够条件下的优化目标函数;
- \(E_l\)部分包含了逆深度期望惩罚项\((d_{pi} - iR_i)^2\),充分考虑了周围点逆深度的平滑性;
- \(\alpha\)代表调节正则化项部分的超参数,从而在一定程度上改变优化的侧重方向;
针对\(E_l\)的惩罚项部分,求得其雅可比矩阵和海塞矩阵如下:
$$
\frac{\partial{E_l^{p_j}}}{\partial{x}}=J_l^{p_j}=
\begin{bmatrix}
\mathbf{0_{1\times6}} & 0 & 0 & d_{pi}-iR
\end{bmatrix}
\\
\frac{\partial^2{E_l^{p_j}}}{\partial{x^2}} = H_l^{p_j} =
\begin{bmatrix}
\mathbf{0_{6\times6}} & \mathbf{0_{6 \times 1}} & \mathbf{0_{6 \times 1}} & \mathbf{0_{6 \times 1}}\\
\mathbf{0_{1\times6}} & 0 & 0 & 0 \\
\mathbf{0_{1\times6}} & 0 & 0 & 0 \\
\mathbf{0_{1\times6}} & 0 & 0 & 1 \\
\end{bmatrix}
$$
3. 基于金字塔的逆深度传递
为了能够方便的表述逆深度传递的重要性,在这部分我会先在3.1小节中梳理一下DSO初始化流程,然后在3.2小节中重点讲解基于金字塔和相邻点的逆深度传递过程。
3.1 DSO初始化过程
下图中,使用虚线框标注出来的部分是DSO初始化器的主要工作流程,值得注意的是,在初始化点选之后,参考帧\(R_f\)上会得到点\(p_i\in R_f\),这些点\(p_i\)会分布在不同的金字塔层级上,为了方便后续这些点的逆深度传递,DSO构造了这些点的同层相邻点和上层父点之间的关系。
3.2 逆深度传递
DSO的初始化器构造了同层相邻点和上层父点之间的关系,这样会比较方便的执行下面的三种操作:
- 从上层到下层优化过程中,上层父点会向下层子点提供逆深度初值。
- 当优化完成后,下层子点会将充分优化的逆深度初值向上层父点传递,以修正父点逆深度值。
- 由于
DSO初始化器在优化目标函数构建中,考虑了相邻点逆深度连续性,这部分连续性的考虑是由相邻点关系实现的。
在每一步优化结束后,DSO初始化器会更新逆深度值,同样会更新逆深度期望值,期望值的更新考虑了相邻点之间的连续性关系,下面的公式描述了逆深度期望的更新策略:
$$
iR_i=(1-\beta)\times{d_{pi}}_{new}+\beta\times{iR_{mid}^i}\\
iR_{mid}^i={Median}(neighbors(p_i))
$$
其中:
- \(iR_i\)为点\(p_i\)逆深度的更新期望;
- \({d_{pi}}_{new}\)为点\(p_i\)逆深度的优化更新值;
- \(\beta\)为相邻点逆深度连续性置信度,在源码为
0.8;
- \(iR_{mid}^i\)为点\(p_i\)邻居的逆深度期望中值;
DSO初始化器使用同层金字塔K近邻的方式构建同层点和邻居点之间的关系,使用向上层金字塔投影寻找最近邻的方式构建与上层父点之间的关系。
3.3 高斯归一化积
考虑父点向子点传递逆深度过程:除了第一次优化过程外,子点都会有一个相对有效的逆深度优化值,这时父点还会向子点提供一个逆深度。DSO初始化器使用了高斯归一化来耦合这两个逆深度值,高斯归一化积的数学描述如下:
$$
\mu_{c} H_{c}=\sum_{i=0}^N \mu_iH_i\\
H_c=\sum_{i=0}^N H_i
$$
父点向子点传递时,子点不仅仅是逆深度值\(d_{pi}\)发生了改变,子点的逆深度期望\(iR\)同样发生了改变,这个传递过程可以由下面的流程图进行描述:
3.2中的公式同样描述了,流程图中的考虑相邻点\(iR\)的连续性操作。通过这样的操作,可以人为的构造出一个考虑了连续性影响的逆深度期望值出来,从而能够完成后续初始化优化目标函数(会涉及点\(p_i\)的逆深度期望\(iR_i\))的构建。
考虑子点向父点的逆深度传递过程:在3.2小节的描述中,父子点之间的关系构造是通过投影和最近邻实现,因此可能会出现一个父点对应多个子点的情况,这时又会出现多个逆深度值同时出现的问题,DSO仍然是通过高斯归一化积来解决这个问题,下面的流程图描述了具体的传递过程:
4. 初始化器的Schur优化加速
这里我打算以\(t_{ji}\)不足条件下的优化加速为例,初始化中\(t_{ji}\)不足时的优化目标函数如下:
$$
E_f=\sum_{p_i\in R_f}{\sum_{p\in \mathcal{N}_i(p_i)}{||I_j(p')-e^a_{ji}I_{R_f}(p)-b_{ji}||_{\gamma}}}+E_l\\
E_l=\alpha \sum_{p_i\in R_f}{(d_{pi}-iR_{i})^2}
$$
首先,考虑非惩罚部分\(E_{nl}=E_f-E_l\),这部分能量的残差为\(r_k^{nl}=I_j(p')-e^a_{ji}I_{R_f}(p)-b_{ji}\),那么根据高斯牛顿法,在不考虑Huber核函数的情况下,可以构建优化方程:
$$
\begin{align*}
H_{nl}^{p_j} & =\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{x}})^T(\frac{\partial{r_k^{nl}}}{\partial{x}})} \\ & =
\begin{bmatrix}
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{\delta\xi_{ji}}})^T(\frac{\partial{r_k^{nl}}}{\partial{\delta\xi_{ji}}})} &
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{\delta\xi_{ji}}})^T (\frac{\partial{r_k^{nl}}}{\partial{a_{ji}}})} &
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{\delta\xi_{ji}}})^T (\frac{\partial{r_k^{nl}}}{\partial{b_{ji}}})} &
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{\delta\xi_{ji}}})^T (\frac{\partial{r_k^{nl}}}{\partial{d_{pi}}})} \\
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{a_{ji}}})^T(\frac{\partial{r_k^{nl}}}{\partial{\delta\xi_{ji}}})} &
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{a_{ji}}})^T\frac{\partial{r_k^{nl}}}{\partial{a_{ji}}}} &
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{a_{ji}}})^T(\frac{\partial{r_k^{nl}}}{\partial{b_{ji}}})} &
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{a_{ji}}})^T(\frac{\partial{r_k^{nl}}}{\partial{d_{pi}}})} \\
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{b_{ji}}})^T(\frac{\partial{r_k^{nl}}}{\partial{\delta\xi_{ji}}})}&
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{b_{ji}}})^T(\frac{\partial{r_k^{nl}}}{\partial{a_{ji}}})}&
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{b_{ji}}})^T(\frac{\partial{r_k^{nl}}}{\partial{b_{ji}}})}&
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{b_{ji}}})^T(\frac{\partial{r_k^{nl}}}{\partial{d_{pi}}})} \\
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{d_{pi}}})^T(\frac{\partial{r_k^{nl}}}{\partial{\delta\xi_{ji}}})} &
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{d_{pi}}})^T(\frac{\partial{r_k^{nl}}}{\partial{a_{ji}}})} &
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{d_{pi}}})^T(\frac{\partial{r_k^{nl}}}{\partial{b_{ji}}})} &
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{d_{pi}}})^T(\frac{\partial{r_k^{nl}}}{\partial{d_{pi}}})}
\end{bmatrix}
\end{align*}
$$
$$
b_{nl}^{p_j}=-\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{x}})^T \times r_k^{nl}}\quad=
-\begin{bmatrix}
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{\delta\xi_{ji}}})^T \times r_k^{nl}} \\
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{a_{ji}}})^T \times r_k^{nl}} \\
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{b_{ji}}})^T \times r_k^{nl}} \\
\sum_{p \in \mathcal{N_i(p_i)}}{(\frac{\partial{r_k^{nl}}}{\partial{d_{pi}}})^T \times r_k^{nl}}
\end{bmatrix}
$$
$$
H_{nl}=
\begin{bmatrix}
\sum_{p_i \in R_f}{U_{p_j}} & W^{p_0} & W_{p_1} & ... & W_{p_m} \\
W_{p_0} & V_{p_0} \\
W_{p_1} & & V_{p_1}\\
... & & & ... \\
W_{p_m} & & & & V_{p_m}\\
\end{bmatrix}
\quad
b_{nl}=
-\begin{bmatrix}
\sum_{p_i \in R_f}{b_{U}} \\
b_{V_{p_0}} \\
b_{V_{p_1}} \\
... \\
b_{V_{p_m}} \\
\end{bmatrix}
$$
其中:
- \(\frac{\partial{r_k^{nl}}}{\partial{\delta\xi_{ji}}}\)、\(\frac{\partial{r_k^{nl}}}{\partial{d_{pi}}}\)的计算公式在DSO中的优化模型文章中推导过;
- \(\frac{\partial{r_k^{nl}}}{\partial{b_{ji}}}\)、\(\frac{\partial{r_k^{nl}}}{\partial{d_{pi}}}\)的计算公式在本篇文章的第一小节中推导过;
- \(H_{nl}^{pj}\)和\(b_{nl}^{p_j}\),为某个点\(p_i\)投影到\(p_j\)这部分的优化约束;
- \(H_{nl}\)和\(b_{nl}\),为不含惩罚项部分的能量函数总约束,我使用了分块矩阵进行表示,这么做比较方便,矩阵分块结构图如下:
对惩罚项部分,根据文章的第2小节推导的公式,考虑超参数\(\alpha_W\),并使用上图中的分块方式,可以得到惩罚项部分的优化约束矩阵:
$$
H_l= \alpha_W
\begin{bmatrix}
\sum_{p_i \in R_f}{\begin{bmatrix}
I_{3\times 3} & \mathbf{0_{3\times3}} & \mathbf{0_{3 \times 1}} & \mathbf{0_{3 \times 1}}\\
\mathbf{0_{3\times3}} & \mathbf{0_{3\times3}} & \mathbf{0_{3 \times 1}} & \mathbf{0_{3 \times 1}}\\
\mathbf{0_{1\times3}} & \mathbf{0_{1\times3}} & 0 & 0\\
\mathbf{0_{1\times3}} & \mathbf{0_{1\times3}} & 0 & 0\\
\end{bmatrix}} & \mathbf{0_{8\times1}} & \mathbf{0_{8\times1}} & ... & \mathbf{0_{8\times1}}\\
\mathbf{0_{1\times8}} & 1\\
\mathbf{0_{1\times8}} & & 1\\
... & & &...\\
\mathbf{0_{1\times8}} & & & & 1\\
\end{bmatrix}
\\
b_l = -\alpha_W
\begin{bmatrix}
\begin{bmatrix}t_{ji}\\ \mathbf{0_{3\times1}} \\0\\0\end{bmatrix}\\d_{p0}-1\\d_{p1}-1\\...\\d_{pm}-1
\end{bmatrix}
$$
因此整个系统的优化约束为:
$$
H=H_{nl}+H_{l}=
\begin{bmatrix}
\sum_{p_i \in R_f}{U_{p_j}'} & W^{p_0} & W_{p_1} & ... & W_{p_m} \\
W_{p_0} & V_{p_0}+\alpha_W \\
W_{p_1} & & V_{p_1}+\alpha_W \\
... & & & ... \\
W_{p_m} & & & & V_{p_m}+\alpha_W \\
\end{bmatrix}
\quad
b=b_{nl}+b_l=
-\begin{bmatrix}
\sum_{p_i \in R_f}{b_{U}'} \\
b_{V_{p_0}} + \alpha_W(d_{p_0} - 1) \\
b_{V_{p_1}} + \alpha_W(d_{p_1} - 1) \\
... \\
b_{V_{p_m}} + \alpha_W(d_{p_m} - 1) \\
\end{bmatrix}
\\
U_{p_j}'=U_{p_j} + \alpha_W
\begin{bmatrix}
I_{3\times 3} & \mathbf{0_{3\times3}} & \mathbf{0_{3 \times 1}} & \mathbf{0_{3 \times 1}}\\
\mathbf{0_{3\times3}} & \mathbf{0_{3\times3}} & \mathbf{0_{3 \times 1}} & \mathbf{0_{3 \times 1}}\\
\mathbf{0_{1\times3}} & \mathbf{0_{1\times3}} & 0 & 0\\
\mathbf{0_{1\times3}} & \mathbf{0_{1\times3}} & 0 & 0\\
\end{bmatrix}
\quad
b_{U}'=b_{U} + \alpha_W \begin{bmatrix}t_{ji}\\ \mathbf{0_{3\times1}} \\0\\0\end{bmatrix}
$$
最后,根据SLAM十四讲p249页描述的Schur分解公式,先将涉及逆深度部分分解掉,求解相对位姿和相对仿射参数的增量,然后将相对位姿增量和相对仿射参数增量再次带入涉及逆深度方程的部分,求解得到逆深度增量即可。
大矩阵Schur和小矩阵Schur
在上面的推导中,初始化器总优化约束的\(H\)矩阵和\(b\)矩阵由所有投影关系\(p_j\)-\(p_i\)的优化约束\(H_{p_j}\)和\(b_{p_j}\)得到。同样不难证明,大矩阵\(H\)和\(b\)进行Schur分解和所有小矩阵\(H_{p_j}\)和\(b_{p_j}\)分别Schur分解然后组合拼接(这里直接累加即可,因为分解后的矩阵的约束变量是相同的)的效果是一样的。DSO的源码里面也利用了这个结论,从而避免了大稀疏矩阵构建导致的高空间复杂度问题。
喜欢这篇文章吗?喜欢就分享吧:
Twitter
❄ Facebook
❄ Email